• komplexe Zahlen

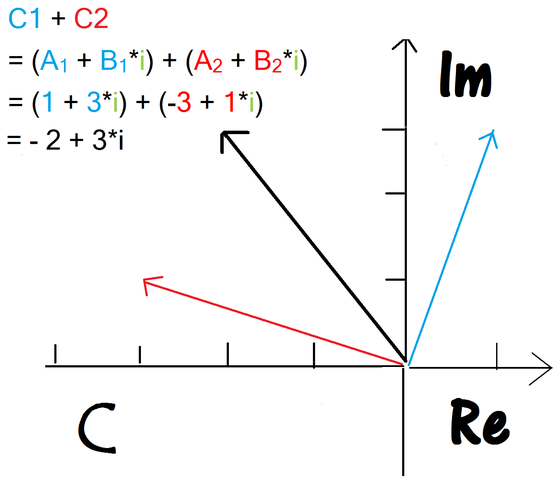
C1 + C2

= (A₁ + B₁*i) + (A₂ + B₂*i)

= A₁ + A₂ + B₁*i + B₂*i

= (A₁ + A₂) + i*(B₁ + B₂)

= Realteil + Imaginärteil

Möchte man komplexe Zahlen in der Gaußschen Zahlenebene addieren,

muss man nichts weiter machen als eine gewöhnliche Vektoraddition.

C1 - C2

…

= (A₁ - A₂) + i*(B₁ - B₂)

= Realteil - Imaginärteil

Möchte man komplexe Zahlen in der Gaußschen Zahlenebene voneinander subtrahieren,muss man nichts weiter machen als eine gewöhnliche Vektorsubtraktion. Quasi das Gleiche wie beim Addieren, nur mit Abziehen statt zusammenzählen.

C1 * C2

= (A₁ + B₁*i) * (A₂ + B₂*i)

= (A₁ * A₂) + (A₁ * B₂*i) + (A₂ * B₁*i) + (B₁*i * B₂*i)

Anmerkung: i * i = -1

= (A₁ * A₂) + (A₁ * B₂*i) + (A₂ * B₁*i) – (B₁ * B₂)

= (A₁ * A₂ - B₁ *B₂) + i *(A₁ * B₂ + A₂ * B₁)

= Realteil + Imaginärteil

C1 / C2

= (A₁ + B₁*i) / (A₂ + B₂*i)

= (A₁ + B₁*i)*(A₂ - B₂*i)

 / (A₂ + B₂*i) *(A₂ - B₂*i)

= (A₁*A₂ + B₁*i*B₂*i) / (A₂² + B₂²)

= ((B₁*A₂ – A₁*B₂) / (A₂² + B₂²)) * i

= Realteil + Imaginärteil

zum vorherigen Blogeintrag                                                                                     zum nächsten Blogeintrag 

Liste aller bisherigen Blogeinträge