Das Einstein-Podolsky-Rosen-Paradoxon (kurz: EPR-Paradoxon, auch: EPR-Effekt) ist ein Argument für die Unvollständigkeit der Quantenmechanik, das durch das Verhalten verschränkter Zweiteilchen-Systeme bei der Messung eines der Teilchen illustriert wird.
1. Einstein, Podolsky und Rosen
1.1. EPR-Experiment
Das Argument wurde nach seinen Urhebern Albert Einstein, Boris Podolsky und Nathan Rosen benannt. Diese skizzierten zunächst ein Gedankenexperiment, das in Folge vielfach rezipiert, umformuliert und schließlich auch umgesetzt wurde.
EPR-artige Experimente weisen folgende Charakteristika auf:
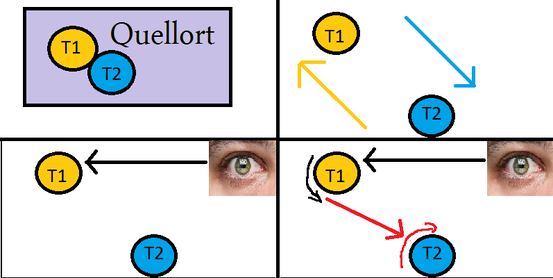
1. Es gibt zwei Teilchen T1 und T2, die anfänglich direkt miteinander wechselwirken und sich daraufhin weit voneinander entfernen. Die Quantenmechanik beschreibt dieses Zweiteilchen-System durch einen einzigen, verschränkten Zustand.
2. Die räumlich getrennten Teilchen besitzen komplementäre Messgrößen (z.B. Ort und Impuls).
3. Wenn sich nach der Messung an T1 dieses Teilchen am Ort A befindet, dann kann der Ort B von T2 mit Sicherheit vorhergesagt werden.
1.2. EPR-Argument
Das EPR-Argument baut auf den folgenden Annahmen auf:
1. In einer vollständigen Theorie muss jedes Element der physikalischen Realität eine Entsprechung haben.
2. Ein Element der Realität ist eine physikalische Größe, deren Wert vorhergesagt werden kann, ohne dass System zu stören.
Ort und Impuls sind zwei physikalische Größen. Jedoch können sie nach der Heisenbergschen Unschärferelation nicht gleichzeitig vorhergesagt werden, weshalb die Quantenmechanik eine unvollständige Theorie sein muss.
1.3. Kritik
Die Unvollständigkeit legt die Existenz verborgener Variablen nahe, die den im Formalismus der Quantenmechanik nicht berücksichtigten Elementen der Realität entsprechen. In der Tat hat Einstein seit der EPR-Arbeit 1935 bis zu seinem Tod 1955 versucht, die Quantenmechanik um lokale Variablen zu vervollständigen.
1964 stellte John Stewart Bell aber die Bellsche Ungleichung auf. Wenn ein von ihm vorgeschlagenes Experiment an verschränkten Teilchen seine Ungleichung bestätigt, hat Einstein recht. Wenn Einstein aber nicht Recht hat, wird das Experiment die Ungleichung verletzen.
Alain Aspect realisierte 1982 das von Bell vorgeschlagene Experiment und zeigte auf, dass es die Bellsche Ungleichung verletzt. Seitdem gelten Einsteins Theorie lokaler verborgener Variablen sowie der ihr zugrunde liegende lokale Realismus als falsifiziert.
D.h. mindestens eines dieser zwei Prinzipien gilt nicht für die Quantenmechanik:
1. Realismus: Physikalische Größen liegen unabhängig von der Messung vor.
2. Lokalität: Physikalische Zustände können sich gegenseitig nur über den Raum und höchstens mit Lichtgeschwindigkeit beeinflussen.
Nach der Kopenhagener Interpretation ist die Quantenmechanik sogar weder realistisch noch lokal: Wenn der Ort von T2 nicht unabhängig von der Messung an T1 vorliegt, dann ist der Realismus verletzt. Dann würde selbst wenn sich T1 und T2 an entgegengesetzten Enden im Universum befänden, eine Ortsmessung an T1 ohne Zeitverzögerung den Ort von T2 festlegen. Das verletzt nicht nur die Lokalität, sondern hat auch eine anhaltenden Debatte über die Verträglichkeit mit der Spezieller Relativitätstheorie ausgelöst.
Die Bohmsche Mechanik widerspricht der Lokalität und hält dafür am Prinzip des Realismus fest. Nach ihr ist der Ort eines Teilchens unabhängig von der Messung real, die Quantenmechanik müsste aber erst um verborgene, indes nicht-lokale Variablen ersetzt werden, um diesen zu erfassen. Auch die Viele-Welten-Interpretation beruht auf solchen nicht-lokalen verborgenen Variablen. Wenn eine dieser Theorien wahr sein sollte, ist die Quantenmechanik deterministisch und Einstein hatte mit seiner anfänglichen Intuition doch Recht: "Gott würfelt nicht."
 Philoclopedia
Philoclopedia
Kommentar schreiben