Das Deduktiv-Nomologische-Modell (kurz: DNM) ist ein Covering-Law Modell der (wissenschaftlichen) Erklärung. Es wurde bereits von Karl Popper in Logik der Forschung (1935) angewendet und durch Carl Gustav Hempel und Paul Oppenheim in "Studies in the Logic of Explanation" (1948) erstmals formalisiert und ist deshalb auch als Hempel-Oppenheim-Schema bekannt.

 „Die Frage „Warum tritt das Phänomen auf?“

wird aufgefasst als Frage „Nach welchen allgemeinen Gesetzen

und aufgrund welcher Vorbedingungen tritt das Phänomen auf?““
- C. G. Hempel und P. Oppenheim: Studies in the Logic of Explanation, S. 136

Laut dem Deduktiv-Nomologischen-Modell besteht eine Erklärung aus[1]:

1.    Explanandum: Satz über das zu Erklärende (Messung, Beobachtung).

2.    Explanans: Sätze über das Erklärende, d.h. über allgemeine Gesetzesaussagen (z.B. Naturgesetz, Theorie) und Rand- bzw. Anwendungsbedingungen (Ursache, Antezedensaussagen).

Dabei wird in einem korrekten deduktiven Argument vom Explanans (als Prämissenmenge) auf das Explanandum (die Konklusion) geschlossen: 

D.h. eine Erklärung besteht in einem Nachweis, der das Explanandum E als (k)einen speziellen Fall allgemeiner Gesetzmäßigkeiten G unter den gegebenen besonderen Bedingungen A auszeichnet.

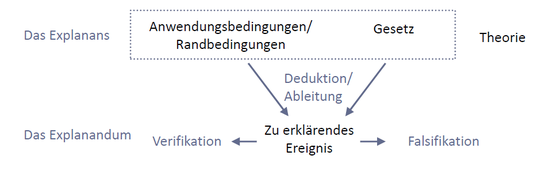
Das Explanans ist eine hinreichende Bedingung für das Explanandum. Aus diesem Grund sind Erklären und Prognostizieren im Deduktiv-Nomologischen-Modell formell identisch. Wenn das Explanandum gegeben ist, lässt es sich aufgrund des Explanans erklären. Wenn das Explanandum aber nocht nicht gegeben ist, kann man es aufgrund des Explanans prognostizieren.

Ein Beispiel:

(G1) Wenn die Temperaturen unter null Grad fallen, gefriert Wasser.
(G2) Wenn Wasser gefriert, dehnt es sich aus.
(G3) Wenn ein geschlossenes Objekt voll von Wasser ist und sich das Wasser weiter ausdehnt, platzt das Objekt.
(A1) Die Temperatur ist gestern unter null Grad gefallen.
(A2) Die Regentonne hinter dem Haus war voll von Wasser.
(A3) Die Regentonne hinter dem Haus ist ein geschlossenes Objekt.
______________________________________________________
(E) Die Regentonne hinter dem Haus ist geplatzt.

Das Explanandum, d.h. das Phänomen, das erklärt werden soll, ist die geplatzte Regentonne hinter dem Haus. Um es zu erklären, benötigen wir einerseits allgemeine Gesetzesaussagen wie jene, dass Wasser unter Null Grad gefriert (G1), sich in diesem Fall ausdehnt (G2) und geschlossene Objekte voller sich ausdehnenendem Wasser platzen (G3). Da es bei unserer Erklärung aber nicht um Wasser und Objekte im Allgemeinen geht, sondern um den konkreten Fall der Regentonne hinter dem Haus, benötigen wir noch weitere, den vorliegenden Fall spezifierende Antecedensbedingungen: Die Temperatur ist gestern unter null Grad gefallen (A1), die Regentonne war voller Wasser (A2) und sie ist ein geschlossenes Objekt (A3). Nun haben wir alle Konstituenten zusammen, um folgende deduktiv-nomologische Erklärung zu formulieren: Die Regentonne hinter dem Haus ist geplatzt, weil (G1) bis (G3) und weil (A1) bis (A3).

Eine deduktive Form allein reicht aber nicht aus. Eine Erklärung muss zusätzlich die folgenden Adäquatsheitsbedingungen erfüllen[2]:

1.    Folgerungsbedingung: Das Explanandum muss eine logische Konsequenz des Explanans sein.

2.    Gesetzesbedingung: Das Explanans muss allgemeine Naturgesetze enthalten, die zur Ableitung des Explanandums notwendig sind.

3.    Gehaltsbedingung: Das Explanans muss empirischen Gehalt haben, d.h. es muss falsifizierbar sein.

4.    Wahrheitsbedingung: Die Sätze, welche das Explanans konstituieren, müssen wahr sein.

Die Folgerungsbedingung besagt, dass eine Erklärung nur dann brauchbar ist, wenn es sich um ein folgerichtiges deduktives Argument handelt, d.h. wenn das Explanandum aus dem Explanans logisch folgt beziehungsweise ableitbar ist.

Die Gesetzesbedingung besagt, dass eine Erklärung nur dann als wissenschaftlich gelten kann, wenn in ihr zumindest ein Naturgesetz vorkommt, ohne das sich das Explanandum nicht aus dem Explanans ableiten ließe.

Die Gehaltsbedingung besagt, dass es möglich sein muss, aus den Aussagen, die in ihrer Gesamtheit das Explanans ergeben, Vorhersagen abzuleiten, die zumindest im Prinzip durch Experiment oder Beobachtung überprüfbar sind.

Und die Wahrheitsbedingung besagt, dass Folgerichtigkeit nicht genügt, die Prämissen der Erklärung müssen zusätzlich noch inhaltlich wahr sein.

Eine Erklärung, welche die Bedingungen (1) - (4) erfüllt, heißt wahre Erklärung.

Erklärung, welche die Bedingung (1) - (3) erfüllt, heißt potentielle Erklärung. Sie würde das Explanandum erklären, wenn ihre Prämissen wahr wären.

Das Deduktiv-Nomologische-Modell war seinerseits der erste großangelegte Versuch, den Begriff der wissenschaftlichen Erklärung selbst zu erklären.

Im Laufe der Zeit wurden aber zahlreiche fundierte Kritikpunkte an ihm laut:

Das "Pre-Emption"-Problem kann anhand dieser Erklärung erörtert werden:[3]

(A1) Jones hat ein Kilo Arsen zu sich genommen.
(G1) Wenn man ein Kilo Arsen zu sich nimmt, stirbt man innerhalb der darauffolgenden 24 Stunden.
_______________________
(E) Jones ist innerhalb der darauffolgenden 24 Stunden gestorben.

Diese Erklärung für den Tod von Jones entspricht in jeder Hinsicht dem Deduktiv-Nomologischen-Modell:

1.    Folgerichtigkeitsbedingung: Es handelt sich um ein folgerichtiges Argument.

2.    Gesetzesbedingung: Die Prämissenmenge enthält eine allgemeine Gesetzesaussage (G1).

3.    Gehaltsbedingung: Die Prämissenmenge ist empirisch gehaltvoll.

4.    Wahrheitsbedingung: Die Prämissen sind wahr (Annahme).

Das Problem der 'pre-emption' (des Zuvorkommens) liegt nun aber darin, dass Jones zwar tatsächlich ein Kilo Arsen zu sich genommen hat und tatsächlich innerhalb der darauffolgenden 24 Stunden verstorben ist, dies aber nicht aufgrund des Arsenkonsums, sondern aufgrund eines Autounfalls. Es ist wahr, dass das Arsen Jones getötet hätte, wäre der Autounfall nicht passiert. Das ändert aber nichts daran, dass die obige Erklärung, die das Ableben Jones' auf seinen Arsenkonsum zurückführt, falsch ist, obwohl alle Bedingungen des Deduktiv-Nomologischen-Modells erfüllt sind.

Das "explanatorische Irrelevanz"-Problem zeigt sich an dieser Erklärung[4]:

(A1) Jones hat die Antibabypille genommen.
(G1) Wenn man die Antibabypille nimmt, wird man nicht schwanger.
_______________________________________________________
(E) Jones ist im letzten Jahr nicht schwanger geworden.

Auch hier sind alle Adäquatheitsbedingungen des Deduktiv-Nomologischen-Modells erfüllt und trotzdem handelt es sich num keine akzeptable Erklärung. Denn Jones nicht-Schwangersein liegt an seinem Geschlecht, das Explanans ist zur Erklärung des Explanandums irrelevant.

Das "Akzidentielle Verallgemeinerung"-Problem liegt in der zweiten AB:

2.    Gesetzesbedingung: Das Explanans muss allgemeine Naturgesetze enthalten, die zur Ableitung des Explanandums notwendig sind.

Das wirft eine offenkundige Frage auf: Was sind Naturgesetze? Und wie erkennt man sie? Nach Carl Gustav Hempel sind Naturgesetze "Aussagen universeller Form", in denen zum Ausdruck kommt, "dass, wo und wann auch immer Bedingungen einer bestimmten Art F eintreten, immer und ohne Ausnahme auch gewisse Bedingungen einer anderen Art G eintreten werden."[5] Naturgesetze zeichnen sich nach Hempel also durch die folgende Form aus:

Für alle x: Wenn x ein F ist, dann ist x auch ein G.

Diese Definition hat aber ein Problem. Die folgenden beiden Beispiele entsprechen nach Hempel der Form eines Naturgesetzes[6]:

a. Für alle x: Wenn x ein Klumpen angereichertes Uran ist, dann hat x einen Durchmesser, der kleiner ist als ein Kilometer.

b. Für alle x: Wenn x ein Klumpen Gold ist, dann hat x einen Durchmesser, der kleiner ist als ein Kilometer.

Beide Aussagen sind Allaussagen und wahr. Der entscheide Unterschied ist:

Aussage (a) ist notwendig wahr, weil die kritische Masse von ²³⁵U bei 50 Kilogramm liegt und uns größere Uranklumpen deshalb um die Ohren fliegen würden.

Aussage (b) ist kontingent wahr, da es (nach unserem Wissen) zwar keinen Goldklumpen gibt, der breiter ist als ein Kilometer, es ihn aber geben könnte.

Anders als Aussage (a) ist (b) also bloß eine akzidentielle Verallgemeinerung.

Aussage (b) ist somit kein Naturgesetz, obwohl es der universellen Form nach Hempel genügt. Die universelle Form stellt also eine notwendige, aber keine hinreichende Bedingung für eine naturgesetzliche Form dar: "[E]in wissenschaftliches Gesetz [lässt sich] nicht adäquat als eine wahre Aussage universeller Form definieren."[7]

Dies wirft aber eine nahe liegende Frage auf: Was unterscheidet Naturgesetze von bloß akzidentiellen Verallgemeinerungen? Diese Frage ist nicht nur für sich genommen, sondern auch in Bezug auf das Deduktiv-Nomologische-Modell wichtig: Denn wenn alle Erklärungen ein Naturgesetz beinhalten müssen, dann müssen wir auch imstande sein, Naturgesetze von akzidenziellen Verallgemeinerungen abzugrenzen. Das sind wir momentan aber nicht.

Das "Erklärungsasymmetrie"-Problem zeigt sich an dieser Erklärung:[8]

(A1) Der Fahnenmast ist x Zentimeter hoch.
(A2) Die Sonne steht in einem Winkel von y Grad hinter dem Fahnenmast.
(G1) In einem homogenen Medium breiten sich Lichtstrahlen geradlinig aus.
_____________________________________________________________
(E) Der Schatten des Masts ist z Zentimeter lang.

Dieser Erklärung entspricht dem Deduktiv-Nomologischen-Modell: Die Höhe des Fahnenmasts und der Winkel, in dem die Sonne hinter dem Fahnenmast steht, sind die notwendigen Antecedensbedingungen. Und das Gesetz der geradlinigen Ausbreitung des Lichts (G1) stellt ein allgemeines Naturgesetz dar.

Sehen wir uns nun aber die folgende Erklärung an:

(A1) Der Schatten des Fahnenmasts ist z Zentimeter lang.
(A2) Die Sonne steht in einem Winkel von y Grad hinter dem Fahnenmast.
(G1) In einem homogenen Medium breiten sich Lichtstrahlen geradlinig aus.
_____________________________________________________________
(E) Der Fahnenmast ist x Zentimeter hoch.

Auch diese Erklärung entspricht dem DNM. Doch im Gegensatz zur vorhergehenden Erklärung, sind hier Explanandum und (A1) vertauscht wurden. D.h. u.a. die Höhe des Fahnenmastes soll durch den Einfallswinkel der Sonne und die Länge des Schattens erklärt werden, was vielen absurd erscheint. Während die Länge des Fahnenmasts zusammen mit den anderen Informationen ohne Zweifel erklärt, warum der Schatten z Zentimeter lang ist, kann die Länge des Schattens ganz klar nicht als eine Erklärung für die Höhle des Fahnenmasts herangezogen werden.[9] Aus der Perspektive des DNM ist jedoch vollkommen rätselhaft, warum die Erklärung nur in eine Richtung funktionieren sollte, weil beide Erklärungen sämtlichen Adäquatheitsbedingungen vollauf entsprechen. Im Rahmen des DNMs lässt sich also nicht verständlich machen, warum die erste Erklärung akzeptabel ist, die zweite hingegen nicht.

[1] Carl Gustav Hempel: Aspects of Scientific Explanation, S. 247

[2] Carl Gustav Hempel: Aspects of Scientific Explanation, S. 247

[3] Peter Achinstein: The Nature of Explanation, S. 168 - 173

[4] Wesley Salmon: A Third Dogma of Empiricism, S. 95 - 107 

[5] Carl Gustav Hempel: Philosophie der Naturwissenschaften, S. 78

[6] Bas van Fraassen: Laws and Symmetry, S. 27

[7] Carl Gustav Hempel: Philosophie der Naturwissenschaften, S. 80

[8] Sylvain Bromberger: Why-Questions

[9] Fragt man, weshalb der Schatten z Zentimeter lang ist, dann ist: "weil der Fahnenmast x Zentimeter lang ist" eine zufriedenstellende Antwort. Fragt man hingegen, weshalb der Fahnenmast x Zentimeter lang ist, wird man "weil der Schattem z Zentimeter lang ist" kaum als befriedigende Erklärung ansehen.

C. G. Hempel, Paul Oppenheim: Studies in the Logic of Explanation (1948)

C. G. Hempel: The Theoretician's Dilemma (1965)

C. G. Hempel: The Function of General Laws in History (1965)

C. G. Hempel: Aspects of Scientific Explanation (1965)

C. G. Hempel: Philosophie der Naturwissenschaften (1974)

W. C. Salmon: Four Decades of Scientific Explanation (1989)

D. H. Ruben: Explaining Explanation (1990)

N. Koertge: Review Article: Explanation and its Problems (1993)

G. Schurz: Scientific Explanation: A Critical Survey (1995)

N. Rescher: H20: Hempel-Helmer-Oppenheim (1997)

J. H. Fetzer: Science, Explanation, and Rationality. Aspects of the Philosophy of Carl G. Hempel (2000)

T. Bartelborth: Erklären (2007)

J. Woodward: Scientific Explanation (2011)

M. Curd: Carl G. Hempel: Logical Empiricst (2012)

Erklärung

Erklärungslücke

Hempel-Paradoxon

Deduktion

Naturgesetz

Gavagai

Internet Encyclopedia of Philosophy

Stanford Encyclopedia of Philosophy

Wikipedia (engl.)

zum vorherigen Blogeintrag                                        zum nächsten Blogeintrag 

Liste aller Blogbeiträge zum Thema "Wissenschaftsphilosophie"