Beispiel: In einer Stadt fahren 100 Taxis, 85 blaue und 15 grüne. Ein Zeuge hat einen Unfall beobachtet, in den ein Taxi verwickelt war. Er sagt, das Taxi sei grün gewesen. Tests ergaben, dass dieser Zeuge unter den gegebenen Sichtverhältnissen jede der beiden Farben in 80% der Fälle richtig identifizierte, und in nur 20% der Fälle mit der jeweils anderen Farbe verwechselte.
Argument: Also war es ein grünes Taxi.
Frage: Wie stark ist dieses Argument?
Mehrheitsmeinung: Daniel Kahnemann und Amos Tversky haben empirisch nachgewiesen, dass die meisten Menschen die Stärke dieses Argumentes auf 0,8 einschätzen. Schließlich haben die Tests ergeben, dass der Zeuge zu 80% zuverlässig ist!
Aber stimmt das?
Es sei: T ≡ Das Taxi war grün. Z ≡ Der Zeuge bezeugt, das Taxi sei grün gewesen.
Dann gilt:

Also: Das Argument ist in Wirklichkeit viel schwächer (0,414 statt 0,8)! Die Mehrheit unterliegt hier also einem Fehlschluss zum Opfer. Dieser Fehlschluss wird auch als Basisraten-Fehlschluss bezeichnet.
Denn: Wer das Argument für stark hält, ignoriert, dass es zwei Möglichkeiten gibt, wie das Zeugnis zustande gekommen sein kann: Das Taxi kann grün gewesen sein und der Zeuge dies richtig erkannt haben, oder es kann blau gewesen sein und der Zeuge sich geirrt haben. Wegen der viel größeren Grundhäufigkeit der blauen Taxis (Basisrate) ist der zweite Fall insgesamt wahrscheinlicher als der erste!
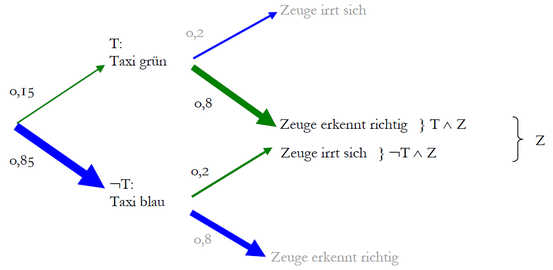
Stellen Sie sich vor: Das gesamte Unfall- und Bezeugungsszenario würde sich 1000-mal wiederholen. Dann würde der Zeuge in 290 Fällen behaupten, das Taxi sei grün gewesen. In nur 120 davon wäre es tatsächlich grün gewesen. 120 : 290 = 0,414.
Der Basisraten-Fehlschluss ist ein relevantes Problem. Denn er droht bei vielen sehr bedeutsamen Anwendungen.
Frage: Wie wahrscheinlich ist es, dass Franz tatsächlich an der seltenen Krankheit leidet?
Es sei: K º Die Krankheit liegt tatsächlich vor; T º Das Testergebnis ist positiv.

Also: In der geschilderten Situation beträgt also die Wahrscheinlichkeit, dass Peter tatsächlich an der Krankheit erkrankt ist, allein auf Grundlage des Testergebnisses nur rund 9%!
Der Fehlschluss des Spielers ist sehr weit verbreitet und beruht auf mindestens zwei irreführenden Intuitionen. Die erste Intuition: Auf lange Sicht müssen 50 % aller Drehs Schwarz ergeben. Da dies nun schon so lange nicht passiert ist, muss jetzt endlich einmal Schwarz kommen, damit die Balance gewahrt bleibt.
Die erste Intuition ist aber irreführend: Insbesondere die Häufigkeits-Interpretation der Wahrscheinlichkeit legt nahe, dass auf lange Sicht der Anteil von Schwarz gegen 50% gehen muss – aber selbst bei Zugrundelegung dieser Interpretation sagt uns die Wahrscheinlichkeitstheorie nichts darüber, wie lange dies dauert. Der „Ausgleich“ kann jetzt gleich oder in 100 Jahren beginnen.
Die zweite Intuition, die beim Fehlschluss des Spielers eine Rolle spielt, ist die folgende:
Zehnmal hintereinander rot:

Ist schon ein sehr unwahrscheinliches Ereignis!
Elfmal Rot,

muss ja dann noch unwahrscheinlicher sein!
Diese zweite Intuition ist aber ebenfalls irreführend: Tatsächlich ist zehnmal Rot in einem gewissen Sinne sehr unwahrscheinlich. Es ist eine von 210 Möglichkeiten, wie 10 Drehs hinsichtlich Schwarz und Rot ausgehen können und in dem Sinn beträgt seine Wahrscheinlichkeit nur 1 : 210 = 1/1024. Nur: Jede andere genaue Schwarz-Rot-Abfolge, z.B.

Ist genauso unwahrscheinlich! Und elfmal Rot,

ist tatsächlich mit 1:211 = 1 / 2048 insgesamt noch unwahrscheinlicher, aber genauso unwahrscheinlich wie zehnmal Rot und dann einmal Schwarz:

 Philoclopedia
Philoclopedia
Kommentar schreiben