Die Hypothetisch-Deduktive Methode ist ein Schema erfahrungs-wissenschaftlicher Geltungsprüfung. Dabei wird die Richtigkeit [oder Falschheit] einer Hypothese anhand ihrer beobachtbaren Konsequenzen untersucht.
„Man unterstellt hypothetisch die Gültigkeit der Annahme und leitet deduktiv Folgen für empirisch zugängliche Phänomene ab. Die Beurteilung der Annahme stützt sich dann auf die Übereinstimmung dieser Folgen mit der Beobachtung.“
- Martin Carrier: hypothetisch-deduktiv. In: Mittelstraß, Band 3, 2008, S. 492
1. Die Schritte der Methode
1.1. Erster Schritt: Bildung einer Hypothese
Die Vertreter der Hypothetisch-Deduktiven Methode betonen, dass wissenschaftliche Hypothesen frei gebildet werden können. Sie brauchen insbesondere nicht durch schon gemachte Beobachtungen nahegelegt zu werden. Damit stehen sie im direkten Widerspruch zu Induktivisten wie Francis Bacon.
Eine methodologische Folge hieraus ist, dass die Entdeckung einer Hypothese nicht von wissenschaftlichen oder logischen, sondern wenn von psychologischen und sozialen Faktoren abhängt. Die Erforschung des Entdeckungszusammenhangs ist daher auch nicht Sache der Wissenschaftstheorie, sondern der Psychologie.
Dies ist jedoch wissenschaftshistorisch unplausibel, da neue Hypothesen häufig vor dem Hintergrund vergangener Beobachtungen aufgestellt wurden!
1.2. Zweiter Schritt: Deduktion der beobachtbaren Konsequenzen
Die Wahrheit einer Hypothese kann (oft) nicht direkt in der Erfahrung evaluiert werden. Daher sollen im Hypothetisch-Deduktiven Modell aus der gebildeten Hypothese empirisch überprüfbare Konsequenzen deduziert.
Die empirisch überprüfbaren Konsequenzen ergeben sich nun aber nicht aus der Hypothese allein! Denn die Hypothese ist erstens in einem größeren theoretischen Kontext (Hintergrundannahmen) eingebettet und kann zweitens nur im Kontext gegebener Umstände (Anfangsbedingungen) getestet werden.
Wenn wir all dies hinzuziehen, ergibt sich dieses Schema vom zweiten Schritt:
H (Testhypothese)
A (Hintergrundannahmen)
I (Anfangsbedingungen)
_______________________
E (Beobachtungsvoraussage)
Eine Beobachtungsvoraussage E wird in der Regel also nicht einfach aus einer Hypothese H, sondern aus einem komplexen Hypothesenbündel H, A, I deduziert.
Theorienbeladenheitproblem: Die Beobachtung selbst findet auch vor Hinter-grundannahmen statt. Sie kann nie so objektiv sein, wie es das Modell fordert.
Problem statistischer Hypothesen: Aus statistischen Hypothesen können keine sicheren Beobachtungsvorhersagen deduziert werden. Es sind allein probabilistische Vorhersagen möglich.
1.3. Dritter Schritt: Empirische Überprüfung der Voraussage
Die Beobachtungsvoraussage E soll nun in der Erfahrung überprüft werden.
Das kann auf mindestens zwei Wegen geschehen:
Tritt die vorhersagte Beobachtung ein, ist E wahr, andernfalls ist E falsch.
1.4. Vierter Schritt: Schluss von Beobachtung auf Hypothese
Aus der Wahrheit oder Falschheit der Beobachtungsvoraussage soll jetzt auf die Wahrheit oder Falschheit der zugrundeliegenden Hypothese geschlossen werden.
Hypothetisch-deduktive Verifikation:
P1. Aus H folgt E.
P2. E ist wahr bzw. eingetreten.
K1. Also: H ist wahr.
Vertreter: Carl G. Hempel
Hypothetisch-deduktive Falsifikation:
P1. Aus H folgt E.
P2. E ist falsch bzw. nicht eingetreten.
K1. Also: H ist falsch.
Vertreter: Karl Popper
Kritiken:
1. Der linke Schluss ist ein Fehlschluss (Bejahung des Konsequenz)!
2. Das Modell ist viel zu permissiv! Denn sie fasst Beobachtungsvoraussagen als h-bestätigend an, die aber irrelevant für h sind. Beispielsweise lässt sich aus h "h oder p" deduzieren, wobei p eine wahre These wie "morgen geht die Sonne auf" ist. Dann wäre jede Hypothese durch den morgigen Sonnenaufgang bestätigt.
3. Die Prämisse P1 "Aus H folgt E" in beiden Schlüssen ist unwahr. Denn wie das Schema vom zweiten Schritt zeigt, folgt E nicht aus H, sondern aus H, A, I.
Dementsprechend wird mit der Wahrheit oder Falschheit von E auch nicht H, sondern H mit allen Hintergrundhypothesen A1, .... An getestet. Es gilt somit:
- Wenn sich die Beobachtungsvoraussage E nicht bewahrheit, könnte H trotzdem wahr und einer der Hintergrundhypothesen An falsch sein.
- Wenn sich die Beobachtungsvoraussage E bewahrheitet, könnte H trotzdem falsch und eine mit E kompatible Hypothese H2 wahr sein.
Kurzum: Sowohl die Wahrheit (Hempel) als auch die Falschheit (Popper) einer Hypothese ist durch die Wahrheit oder Falschheit ihrer beobachtbaren Konse-quenzen empirisch unterbestimmt. Es kann kein "Experimenta crucis" geben.
„Logik und Erfahrung allein erzwingen nicht
die Verwerfung einer spezifischen Hypothese.“
- Martin Carrier: Wissenschaftstheorie zur Einführung (2006), S. 50.
Man sollte wenn dann also eher von einer Stützung anstatt einer Verifikation und von einer Schwächung anstatt von einer Falsifikation der Hypothese reden.
2. Beispiel
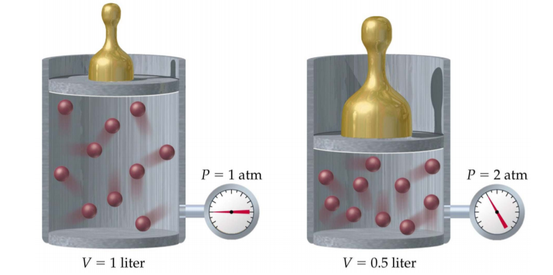
Die Hypothese h sei Boyles Gesetz: Der Druck eines Gases bei konstanter Temperatur ist umgekehrt proportional zu seinem Volumen. Formal:
P x V = konst, vorausgesetzt T = konst.
Daraus lässt sich die empirische Konsequenz e ableiten: Das Anfangsvolumen eines beobachteten Gases ist 1 Liter. Der Anfangsdruck ist 1 atm. Der Druck wird auf 2 atm erhöht. Die Temperatur bleibt konstant. Wenn sich das Volumen auf 0,5, verringert, dann ist Boyles Gesetz gestützt. Ändert sich das Volumen hingegen nicht oder um einen anderen Faktor, so ist Boyles Gesetz geschwächt.
Es gilt eben aber:
- Wenn sich das Volumen nicht um 0,5 verringert, dann ist Boyles Gesetz trotzdem nicht endgültig widerlegt. Denn es könnte eine Anfangs-bedingung falsch gesetzt oder eine Hintergrundhypothese falsch sein.
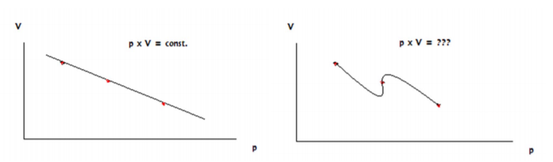
- Wenn sich das Volumen um 0,5 erhöht, dann ist Boyles Gesetz trotzdem nicht endgültig bestätigt. Denn es könnte auch ein anderes Gesetz wahr sein, dass mit dieser Beobachtung verträglich aber mit Boyles Gesetz unverträglich ist:
Siehe auch
zum vorherigen Blogeintrag zum nächsten Blogeintrag
Liste aller Blogbeiträge zum Thema "Wissenschaftsphilosophie"
 Philoclopedia
Philoclopedia
Kommentar schreiben
Philoclopedia (Mittwoch, 15 Januar 2020 01:32)
Statistische Gesetzmäßigkeiten lassen sich in einem H-D-Modell nicht testen!
Angenommen, wir möchten testen, ob der Gang zur Psychotherapie die Wahrscheinlichkeit der Genesung von einem bestimmten neurotischen Syndrom erhöht. Wie könnten wir das anstellen? Wir könnten ein Experiment mit zwei Gruppen von Personen mit dem entsprechenden neurotischen Syndrom durchführen; eine von beiden erhält eine Therapie, die andere nicht.
Problem: Wir können aus dieser Hypothese nicht ableiten, dass die Mitglieder der Therapiegruppe tatsächlich genesen. Wir können lediglich ableiten, dass es wahrscheinlich ist, dass Anzahl der Genesenden in der Therapiegruppe größer ist als die Anzahl der Genesenden in der Gruppe ohne Therapie. Wir können aus der statistischen Hypothese auch nicht ableiten, dass die Anzahl der Genesenden in der Therapiegruppe tatsächlich höher ist als in der Vergleichsgruppe. Wir können lediglich ableiten, dass es wahrscheinlich so ist.
Wahrscheinlichkeiten können in der Regel nicht objektiv gestestet werden. D.h., wir können in einem Einzelfall nicht entscheiden, ob es sich um einen bestätigenden (bzw. widerlegenden) Test handelt!
Philoclopedia (Mittwoch, 15 Januar 2020 02:07)
Statistische Gesetzmäßigkeiten lassen sich in einem H-D-Modell nicht testen!
Angenommen, wir möchten testen, ob der Gang zur Psychotherapie die Wahrscheinlichkeit der Genesung von einem bestimmten neurotischen Syndrom erhöht. Wie könnten wir das anstellen? Wir könnten ein Experiment mit zwei Gruppen von Personen mit dem entsprechenden neurotischen Syndrom durchführen; eine von beiden erhält eine Therapie, die andere nicht.
Problem: Wir können aus dieser Hypothese nicht ableiten, dass die Mitglieder der Therapiegruppe tatsächlich genesen. Wir können lediglich ableiten, dass es wahrscheinlich ist, dass Anzahl der Genesenden in der Therapiegruppe größer ist als die Anzahl der Genesenden in der Gruppe ohne Therapie. Wir können aus der statistischen Hypothese auch nicht ableiten, dass die Anzahl der Genesenden in der Therapiegruppe tatsächlich höher ist als in der Vergleichsgruppe. Wir können lediglich ableiten, dass es wahrscheinlich so ist.
Wahrscheinlichkeiten können in der Regel nicht objektiv gestestet werden. D.h., wir können in einem Einzelfall nicht entscheiden, ob es sich um einen bestätigenden (bzw. widerlegenden) Test handelt!
Philoclopedia (Mittwoch, 15 Januar 2020 02:09)
Hypothetisch-de¬duk¬tive Bestätigung in der
Wissenschaftsgeschichte
Drei Experimente Lavoisiers (1743–1794), dem Urheber der sog. Chemischen Revolution in den 1780er Jahren.
(1) Beobachtung: Gewichtszunahme einiger Metalle beim Rösten im Feuer („Kalzination“): den.
Erklärungsansatz Boyles (1627–1691): Bindung von Feuerteilchen.
Lavoisier: Das Metall nimmt beim Rösten Luft aus der Atmosphäre auf, und es ist dieser zusätzliche Bestandteil, der für das erhöhte Gewicht der Metallkalke verantwortlich ist.
Hypothetisch-de¬duk¬tive Prüfung:
Konsequenz aus Boyles Auffassung: Gewichtszunahme der verschlossenen Retorte.
Konsequenz aus Lavoisiers Ansicht: Keine Veränderung des Gesamtgewichts des Gefäßes.
=> Zwei unterschiedliche Voraussetzungen können auf gegenteilige Konsequenzen führen, von denen sich eine in der Erfahrung bestätigt.
(2) Hauptgegner Lavoisiers: Phlogistontheorie.
Stahl (1660-1734): Verbrennung als Zerlegung: Entweichen von Phlogiston aus dem brennenden Körper; Zurückbleiben unbrennbarer Asche.
Umwandelbarkeit von Metallkalken in die zugehörigen Metalle durch Zufuhr von Phlogiston.
=> Glühen von Bleiglätte (PbO) mit Holzkohle: Entstehen metallischen Bleis.
Dagegen Lavoisier: „Rotes Präzipitat“ (HgO) kann durch bloßes Erhitzen mit dem Brennglas zu metallischem Quecksilber reduziert werden.
Erster Schritt: Rotes Prä¬zipitat als regulärer Quecksilberkalk.
Argument: wenn rotes Präzipitat ein Quecksilberkalk ist, dann sollte seine Reduktion mit Holzkohle zu den gleichen Ergebnissen führen wie die Reduktion anderer Metallkalke.
Die Bestätigung dieser Schlussfolgerung in der Erfahrung stützt hypothetisch-de¬duk¬tiv die Prämisse.
Zweiter Schritt: Reduktion eines Kalks ohne materielle Phlogistonquelle als Anomalie der Phlogistontheorie.
Lavoisier: Kalke als Sauerstoffverbindungen; Reduktion auch ohne äußere Quelle möglich.
=> Einklang mit Lavoisiers Auffassung.
(3) Lavoisier: Wasser kein Element, sondern das Oxid des Wasserstoffs.
Deutung der Verbrennung von Wasserstoff als Wassersynthese.
Hypothetisch-de¬duk¬tive Gegenprobe: Analyse von Wasser.
=> Zerlegung, wenn man dem Sauerstoff im Wasser eine Sub¬stanz zur Bindung anbietet, zu der er eine größere Affinität besitzt als zum Wasserstoff.
Beobachtung: Umwandlung metallischen Eisens in Eisenoxid und Bildung von Wasserstoff.
Unterstellte Reaktion:
Eisen + (Sauerstoff + Wasserstoff) ® (Eisen + Sauerstoff) + Wasserstoff
Wasser Eisenoxid
unknow (Dienstag, 11 Mai 2021 09:32)
Hallo alle hier? Ich bin hier, um hier meine Zeugnisse zu teilen. Dr. Okasia hilft mir, meinen Geliebten zu mir zurückzubringen. Er verzauberte meinen Geliebten mit einem Liebeszauber und kam zu mir zurück, seinem wirklich mächtigen und guten Zauberwirker, an den er glauben konnte. Ich versichere Ihnen, er wird Sie nicht enttäuschen. Ich vertraue ihm mein Leben an, kontaktiere ihn, wenn du irgendwelche Probleme hast. Habt ihr nicht das, was ich noch nie an einen Zauberwirker geglaubt habe, aber jetzt habe ich einen, der mich dazu bringt, an einen Zauberwirker zu glauben. okasiatempleofsolutioncenter@gmail.com oder rufen Sie ihn an, was ihn betrifft +2347026824593