Die Grundidee beim Wunderargument lässt sich ganz gut so zusammenfassen:
Explanandum: Es
gibt bestimmte wissenschaftliche Leistungen oder Eigenschaften, die in einer ersten Annäherung als "wissenschaftlicher Erfolg" bezeichnet werden können und erklärungsbedürftig
sind.
Explanans:
Der wissenschaftliche Realismus ist eine gute
und auch die beste Erklärung für dieses Explanandum.
Es seien S und T Elementaraussagen im Sinne der Aussagenlogik, die entweder wahr oder falsch sind. S sei die Aussage "die Theorie h ist empirisch erfolgreich" und T sei die Aussage "h hat etwas mit der Realität zu tun." Dann ist der allen lokalen Versionen des Wunderargumentes konstitutive Schluss offenbar dieser:
S
______
Also: T
Wenn wir das NMA als probabilistische Schluss verstehen möchten, bemisst sich die Stärke von NMApro am Wert von Pr(T|S). Pr(T|S) ist die bedingte Wahrscheinlichkeit, dass der wissenschaftliche Realismus in Bezug auf h wahr ist, gegeben h ist empirisch erfolgreich. Das heißt auch, dass Pr(T|S) die Wahr-scheinlichkeit anzeigt, mit der das im NMApro erschlossene Explanans korrekt ist.
Wenn diese Bedingung erfüllt ist, ist der Schluss von S auf T somit verlässlich:
(C) Pr(T|S) ≫ 0
Wissenschaftliche Realisten waren sich lange Zeit sicher, dass sie die Bedingung (C) erfüllen können. Diese Sicherheit gründete sich v.a auf diese Überzeugungen:
1. Pr(S) < 0. („der empirische Erfolg der Wissenschaft ist apriori unwahrscheinlich und
deshalb erklärungsbedürftig.“)
2.
Pr(S|¬T) ≪ 0. („der empirische Erfolg der Wissenschaft käme einem Wunder gleich, wenn der wissenschaftliche Realismus nicht wahr wäre.“)
3.
Pr(S|T) ≫ 0. („der empirische Erfolg der Wissenschaft wird durch den wissenschaftlichen Realismus zufriedenstellend erklärt.“)
Colin Howson[1] und später auch P.D. Magnus und Graig Callender[2] haben hier auf einen interessanten Punkt aufmerksam gemacht. Der Wert von Pr(T|S) hängt nämlich nicht nur von Pr(S), Pr(S|¬T) und Pr(S|T), sondern auch von der Basisrate an wahren Theorien Pr(T) ab. Die Kritik lautet also, dass die Proponenten des Wunderargumentes einem Basisraten-Fehlschluss unterlagen.
2. Basisraten-Fehlschluss
Ein instruktiven Beispiel für einen Basisraten-Fehlschluss gibt Howson selbst:
„Suppose that doctors conduct a routine test for a rare disease that occurs
in 1 in a thousand patients. There is virtually no chance that a person with the disease will test negative (i.e. the false negative rate can be regarded as zero). On the other hand, the chance
of a person without the disease testing positive is about 5 % (i.e. the false positive rate is 5 %). A patient takes the test and his result is positive. What is the probability that the patient
has the disease?“
- zitiert nach: Colin Howson: Hume’s problem: Induction and the justification of belief. Oxford: Oxford University Press. 2000, S. 52
Daniel Kahnemann und Amos Tversky haben als erste herausgefunden, dass die meisten Menschen Fragen dieser Art falsch beantworten. Im vorliegenden Beispiel antworten sie mehrheitlich, dass die Wahrscheinlichkeit 95% beträgt. Sie begründen dies mit dem Verweis darauf, dass der Test bei 95% der Menschen mit der Krankheit positiv ausfällt. Dabei verkennen sie jedoch, dass es eigentlich zwei Möglichkeiten gibt, wie das positive Testergebnis zustande gekommen sein kann:
1. Pr(K|P): Der Test ist positiv und der Patient ist krank.
2. Pr(¬K|P): Der Test ist positiv und der Patient ist nicht krank.
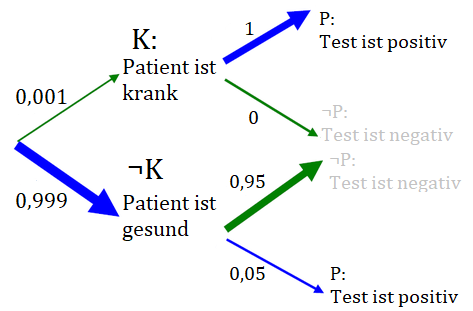
Stellen wir uns vor, der Test wird an tausend Personen durchgeführt. Dann würde er in ungefähr 51 Fällen positiv ausfallen. In nur einem Fall wäre der Patient tatsächlich krank. Also lautet die richtige Antwort nicht 95%, sondern 1/51, also ungefähr 2%! Auch ein Blick auf den Satz von Bayes zeigt auf, dass der Wert von Pr(K|P) funktional von der Basisrate an kranken Menschen Pr(K) abhängt:
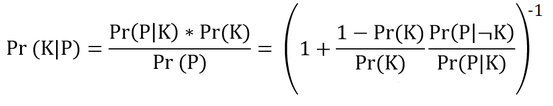
3. Das Wunderargument
Nach Howson haben Realisten analog dazu übersehen, dass es auch wenn eine Theorie empirisch erfolgreich ist, immer zwei Möglichkeiten gibt:
1. eine wissenschaftliche Theorie ist erfolgreich und wahr.
2. eine wissenschaftliche Theorie ist erfolgreich und falsch.
Das könnte sich für den Realisten zu einem ernsthaften Problem entwicklen.[3] Denn nehmen wir zugunsten des Realisten an, dass Pr(S|T) = 1 beträgt. Das heißt, dass jede wahre Theorie auch erfolgreich ist. Weiterhin definieren wir:
s´:= Pr(S|¬T);
h:= Pr(T).
Nun nehmen wir an, dass diese absolute Minimalbedingung für NMApro gelten muss, damit es als ein einigermaßen zuverlässiges Argument gelten kann:
(Cminimal) Pr(T|S) > 0,5
Durch erneute Anwendung von Bayes Theorem können wir das so umformulieren:
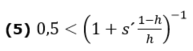
beziehungsweise:
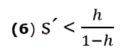
Unsere absolute Minimalbedingung; ausgedrückt in den Ungleichungen (3), (4) und (5); ist für alle Werte von s´ und h unterhalb der blauen Kurve erfüllt:
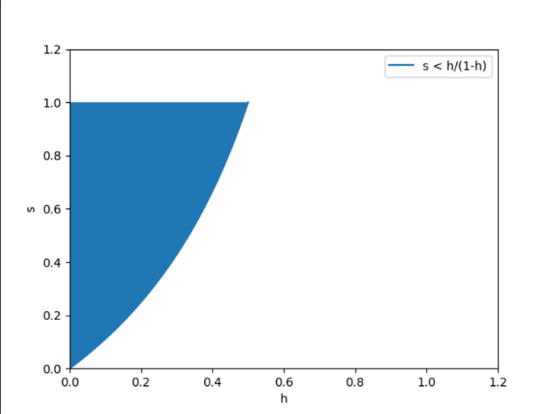
Hier also das Problem für den Realisten: Erstens scheint es prima facie schwer, für einen hohen Wert von h zu argumentieren. Zweitens haben die Proponenten des Realisten – die Antirealisten – lange Zeit hauptsächlich dafür argumentiert, dass der Wert von Pr(S|¬T) nicht sehr niedrig ist. Das Argument der Pessimistischen Meta-Induktion bei Larry Laudan soll zum Beispiel zeigen, dass historisch betrachtet viele wissenschaftliche Theorien erfolgreich waren, die aus heutiger Sicht aber nichts mit der Realität zu tun haben. Dieses und weitere antirealistische Argumente könnten aber wohlmöglich auch dafür verwendet werden, um für einen niedrigen Wert von h bzw. P(T) zu argumentieren: Wenn man sich klar macht, dass eine realistische Sicht auf die allermeisten Theorien heute nicht mehr angemessen ist, könnte das sehr wohl auch für eine niedrige Grundhäufigkeit an wahren Theorien in der Gesamthäufigkeit sprechen.
Lösungsvorschlag
Ich möchte hier einen eigenen Lösungsvorschlag entwickeln. Danach kann der Realist fürs Erste argumentieren, dass der Wert von Pr(T) doch nicht sehr niedrig ist. Pr(T) repräsentiert die Grundhäufigkeit von Theorien, die etwas mit der Realität zu tun haben, in einer relevanten Gesamtpopulation. In Howsons Krankheitsbeispiel wurde der Patient zufällig aus der Population aller Menschen ausgewählt. Aber was wäre, wenn ein Arzt die Personen präselektiert, die typische Krankheitssymptome aufzeigen und nur diese testet? Dann wäre die Basisrate Pr(K) an kranken Menschen in der präselektierten Gesamtpopulation sehr viel höher! Wenn ein Mensch dann positiv getestet wird, ist die so bedingte Wahrscheinlichkeit, dass er krank ist Pr(K|P), ebenfalls sehr viel höher. Der wissenschaftliche Realist kann nun die Annahme vertreten, dass Wissenschaftler Theorien auch nicht zufällig auswählen, sondern durch hochpräzise Experimente unter ähnliches nur die empirisch adäquaten, etc. Theorien präselektieren. Die Basisrate Pr(T) an wahren Theorien ist in der Gesamtpopulation von so präselektierten Theorien höher als in der von zufällig konstruierten Theorien.
Aber das war es noch nicht. Der Realist kann nun, um sein Argument stark zu machen, zwischen lokalen und globalen "Krankheitsargumenten" unterscheiden:
"lokales Krankheitsargument": Ein Patient wird getestet. Der Test war positiv, also ist der Patient zu 95% krank (Basisraten-Fehlschluss!)
"globales Krankheitsargument": Tausende Patienten werden getestet. Der Test ist zu 95% positiv, also wurden die Patienten so präselektiert, dass unter den getesteten Patienten mehr Kranke sind, als wenn man sie zufällig ausgewählt hätte (kein Basisraten-Fehlschluss!)
Lokale Versionen des NMA hingegen haben dieselbe Form wie das "lokale Krankheitsargument". Dementsprechend unterliegen sie dem Basisraten-Fehlschluss. Aber wie wir gesehen haben, ist das vielleicht gar kein Problem. Denn trotzdem könnte Pr(T) > 0 und in Folge auch die Bedingung Pr(T|S) ≫ 0.
Globale Versionen des NMA, wie etwa das von Richard Boyd, haben hingegen häufig die selbe Form wie das globale Krankheitsargument. Sie beginnen beim Umstand, dass tausende moderne wissenschafftliche Theorien empirisch enorm erfolgreich sind. Daraus wird geschlossen, dass wissenschaftliche Theorien durch die wissenschaftliche Methodologie so präselektiert werden, dass unter den selektierten Theorien viel mehr Theorien sind, die etwas mit der Realität zu tun haben, als dies bei einer zufälligen Selektion der Fall wäre. Die relevante Basisrate ist hier die Gesamthäufigkeit an Theorien, die etwas mit der Realität zu tun haben. Diese werden hier nicht ignoriert, sondern stehen gerade im Zentrum von globalen Wunderargumenten. Folglich unterliegen einige der neueren Versionen des Wunderargumentes gar nicht einem Basisraten-Fehlschluss!
Fußnoten
[1] Colin Howson: Induction and the Justification of Belief. Oxford. 2000, Kap. 3
[2] Graig Callender und P.D. Magnus: Realist Ennui and the Base Rate Fallacy. In: Philosophy of Science, 71(3), S. 320–338.
[3] Jan Sprenger: The probabilistic No Miracles Argument. 2015.
 Philoclopedia
Philoclopedia
Kommentar schreiben