Die Verifikationstheorie der Bedeutung ist eine Theorie, oder genauer eine Reihe von Theorieansätzen, die im Logischen Empirismus diskutiert wurden.
Sie bildet den wahrscheinlich wichtigsten Ausgangspunkt für alle späteren Debatten über die Bedeutung speziell wissenschaftlicher Ausdrücke und Sätze.
Sie besagt:
Verifikationstheorie (VT): Die Bedeutung eines nicht-analytischen Satzes besteht in der Methode, mit der sein propositionaler Gehalt (im Prinzip) empirisch überprüft werden kann.
Angewandt auf die Sprache der Wissenschaften besagt die VT Folgendes:
theoretischer Term: Die Bedeutung eines theoretischen Terms PT, der nicht für Beobachtbares steht, ist durch eine Definition von PT gegeben, die angibt, wie im konkreten Fall (im Prinzip) entschieden werden kann, ob der Ausdrucks PT erfüllt ist.
theoretischer Satz: Die Bedeutung eines theoretischen Satzes, der nicht für Beobachtbares steht, ist gegebene durch die Bedeutung seiner Terme (und die Regeln der Logik).
Die wissenschaftliche "Methode der Verifikation" ist in diesem Sinne folglich gegebenen durch die Bedeutung der Terme (plus die Regeln der Logik).
Als formalsprachliche Formulierung für die Definition eines Prädikats PT, der nicht für Beobachtbares steht, hat Rudolf Carnap in einem einfachen Fall den Satz
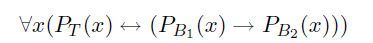
angegeben, wobei PB1 und PB2 Terme sind, die für Beobachtbares stehen.
Diese Form einer Definition ist für thereotische Ausdrücke gedacht, die sich:
- als Dispositionsterme auffassen lassen ("magnetisch", "Katalysator", "spaltbar" u.ä.). Wobei PB1 die Manifestationsbedingungen für die Disposition beschreibt und PB2 die manifeste Eigenschaft.
- und für Ausdrücke für Größen und Eigenschaften, für die man Mess- und Nachweisverfahren hat. Wobei PB1 dass Mess- bzw. Nachweisverfahren beschreibt und PB2 die dabei beobachtbare "Indikatoreigenschaft".
Beispiel: PT könnte für den theoretischen Ausdruck "x hat die Temperatur T" stehen. PB1 steht für "x wird in Kontakt mit dem Quecksilberthermometer QT gebracht". Und PB2 steht für "Das Thermometer QT zeigt für X E Einheiten an".
Kritik: Wenn PB1 nicht erfüllt ist, dann ist (PB1 à PB2) immer wahr.
Lösung: Das Konditional als kontrafaktisches Konditional umformulieren.

Reduktionssätze
Problem: In den Wissenschaften werden die Anwendungsbedingungen PB1 eines Prädikats PT bei der Einführung von PB1 in der Regel nicht ein für alle mal definiert. Stattdessen werden die Anwendungsbedingungen nach und nach für verschiedene Anwendungsbereiche entwickelt und kontinuierlich überarbeitet.
Beispiel: PT steht wieder für "x hat die Temperatur T". Für niedrige Temperaturen in der Nähe des absoluten Nullpunkts worden erst in den letzten Jahrzehnten Messverfahren entwickelt und diese werden nicht über PB2 bzw. QT ausgerichtet.
Wenn für ein großer Teil der in den Wissenschaften gebräuchlichen theoretischen Ausdrücke die Anwendungsbedingungen nicht ein für alle mal festgelegt sind, dann folgt daraus, das sie nach der Verifikationstheorie keine Bedeutung haben.
Die logischen Empiristen zeigten nun zwei Arten von Reaktionen:
Wenn sie diese Konsequenz akzeptierten, wurden sie zu Instrumentalisten.
Wenn sie die Konsequenz nicht akzeptierten, haben sie die strikte Forderung nach der Definierbarkeit von theoretischen Ausdrücken durch die schwächere nach Erläuterung durch sogenannte Reduktionssätze ersetzt.
Ein Reduktionssatz für ein Ausdruck PT soll nur noch die Anwendungsbedingungen x in ganz bestimmten Situationen spezifizieren:
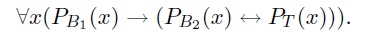
Beispiel: PT(x) steht für "x hat die Temperatur T".Die Formulierung oben besagt: Wenn x in Kontakt mit dem Quecksilberthermometer QT gebracht wird, dann gilt: Das Thermometer zeigt für x E Einheiten an, wenn x die Temperatur T hat.
Problem 1: Wenn die Bedeutung von PT(x) über die Methode seiner Verifikation gegeben ist, bestimmt die Bedeutung von PT(x) nicht seine gesamte Extension.
Beispiel: Die Extension von "x hat die Temperatur T" ist nur noch für Fälle gegeben, in denen ein Quecksilberthermometer in Kontakt mit x gebracht wird.
Man spricht deshalb von partieller Definition und partieller Unbestimmtheit.
Problem 2: Für viele theoretische Ausdrücke lassen sich direkt keine Reduktionssätze angeben. Stattdessen kann man die Anknüpfung an Beobachtung nur dadurch herstellen, dass man bekannte Beziehungen zu anderen Ausdrücken derselben Art ausnutzt, die ihrerseits reduzierbar sind.
Beispiele: Die Hamiltonfunktion und die elektromagnetischen Potentiale.
Problem 3: "PB2(x) ↔ PT(x)" ist einfach nicht wahr.
Beispiel: Wenn x die Temperatur T hat, kann die Anzeige von E Einheiten auf QT gestört wurden sein. Und wenn QT E Einheiten anzeigt, kann dies durch einen anderen Faktor verursacht wurden sein, als dass x die Temperatur T besitzt.
Fazit: Die logischen Empiristen haben die Forderung, dass jeder einzelne "sinnvolle" theoretischer Ausdruck reduzierbar sein muss, aufgegeben zugunsten der, dass die Gesamtheit der Ausdrücke in einer Theorie verifizierbar sein muss:
àDie "Standarddarstellung" wissenschaftlicher Theorien.
 Philoclopedia
Philoclopedia
Kommentar schreiben