Interpretationen der Quantenmechanik
Die Interpretationen der Quantenmechanik deuten die ontologische und epistemologische Bedeutung des (1) mathematischen Formalismus und der (2) Beobachtungen, aus welchen die Quantenmechanik aufgebaut ist.
Zwar gilt die Quantenmechanik als eine der (1) mathematisch präzisesten und (2) empirisch am besten bestätigten erfahrungswissenschaftlichen Theorien überhaupt. Aber aus (1) und (2) geht (derzeit) noch nicht eindeutig hervor, was für eine Realität die Quantenmechanik beschreibt. Ihre Deutungen sind deshalb in der Regel auch experimentell ununterscheidbar und Gegenstand der Metaphysik oder Wissenschaftsphilosophie. Einige Wissenschaftlicher und insbesondere Positivisten halten sie aus diesem Grund für unwissenschaftlich.[1] Es hat sich aber herausgestellt, dass sich zentrale und originär-physikalische Begriffe der Quantentheorie (Messung, Beobachter, Wahrscheinlichkeit, Dekohärenz usw.) ohne interpretativen Rahmen nicht definieren lassen. Andere Köpfe sehen die Formulierung einer konsistenten Deutung der Quantenmechanik deshalb als einen sinnvollen, wenn nicht notwendigen Bestandteil der Theorie an.[2]
Und die IQM stehen auch nicht in einem luftleeren Raum, sondern müssen klaren Bedingungen entsprechen, um ernstgenommen zu werden:
(a) Dem mathematischen Formalismus und den Experimenten der QM.
(b) Der Minimalinterpretation der QM, welche die Theorie
testbar macht.
(c) Sie muss ergänzende Festlegungen treffen, die die IQM individuieren.
Die folgende Tabelle zeigt einen Vergleich der gängigsten IQM[3]:
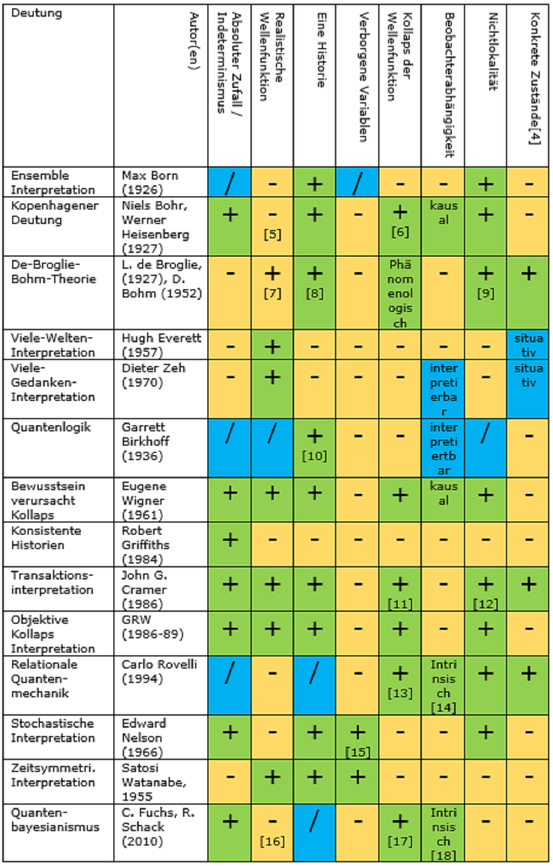
1. Interpretationsrelevante Aspekte
"[…] Es ist sicher zu sagen, niemand versteht Quantenmechanik."
- Richard Feynman: The Character of Physical Law, Kapitel 6
Es gibt eine Reihe von Aspekten und Begriffen in der Quantenmechanik, die nicht nur mit den etablierten Vorstellungen der klassischen Physik brechen, sondern auch der alltäglichen Anschauung zuwiderlaufen. Der Welle-Teilchen-Dualismus ist ein geradezu prädestiniertes Beispiel dafür. Diese Aspekte können zwar in Experimenten beobachtet und in Formeln berechnet werden, ihre tatsächliche Bedeutung versteht aber niemand. Das Doppelspaltexperiment etwa ist recht simpel, was aber in ihm genau abläuft, kann indes niemand erklären. Gleichzeitig scheinen gerade diese Aspekte philosophisch besonders interessant und deshalb intrepretationsrelevant zu sein.
1.1. Determinismus
Die klassische Mechanik gilt gemeinhin als deterministisch.[19] Selbiges gilt für die relativistische Mechanik.[20] Ein laplacescher Dämon könnte aus dem Zustand eines dieser Systeme alle zukünftigen vorausberechnen. Nichtlineare Systeme sind zwar nicht in diesem Sinne vorhersehbar, jedoch ontologisch vorherbestimmt (siehe: deterministisches Chaos). Jegliches anscheinend zufällige Verhalten und jegliche Wahrscheinlichkeit in einer makrophysikalischen Theorie resultieren ausschließlich aus theoretischer Unkenntnis oder experimenteller Unzulänglichkeit.
Anders verhält es sich in der Mikrophysik: Laut der populären Kopenhagener Deutung der Quantenmechanik ist selbige objektiv-indeterministisch.[21] Die Heisenbergsche Unschärferelation beschreibt also eine tatsächliche Unmöglichkeit und die Zukunft ist nicht nur epistemologisch, sondern auch ontologisch unvorherbestimmbar. Die Tatsache, dass es beispielsweise unmöglich ist, den Zeitpunkt des Zerfalls eines einzelnen Radiumatoms vorherzusagen, ist demnach nicht darin begründet, dass der Beobachter nicht alle Informationen hat. Vielmehr scheint es tatsächlich keinen hinreichenden Grund für den konkreten Zeitpunkt des Zerfalls zu geben, der Zeitpunkt erscheint "objektiv zufällig".[22]
Es gibt aber auch einige Interpretationen, die die Quantenmechanik für deterministisch halten. Dazu zählen insbesondere die Viele-Welten-Interpretation und die De-Broglie-Bohm-Deutung. Laut der letzteren Interpretation bietet die Quantenmechanik keine vollständige Beschreibung der Natur, sondern lässt bestimmte Einflussfaktoren außer Betracht (verborgene Variablen). Wüssten wir um alle Einflussfaktoren, könnten wir auch den Zerfall eines einzelnen Radiumatoms vorausbestimmen. Die Frage nach der Determiniertheit oder Indeterminiertheit der Welt spielt in der Debatte um Willensfreiheit und somit auch in rechtsphilosophischen Straf- und politphilosophischen Demokratietheorien eine herausragende Rolle (siehe: Libertarismus, Denkfehler).
1.2. Realismus und Kollaps der Wellenfunktion
In der Quantenmechanik wird der Zustand eines Quantenobjektes durch die Wellenfunktion beschrieben. Diese gibt u.a. an, wie wahrscheinlich es ist, ein Elektron zu einem bestimmten Zeitpunkt an einem bestimmten Ort anzutreffen. Der genaue Zustand kann aber erst durch eine Messung ausgemacht werden. Dass Messproblem besteht nun in der Frage, ob der Zustand des Teilchens vor der Messung (oder Registrierung) nur epistemologisch oder auch ontologisch unbestimmt ist. Wenn er es auch ontologisch ist, könnte der Teilchenzustand beobachterabhängig sein.
Falls die Wellenfunktion prinzipiell mehrere Ergebnisse zulässt, befindet sich das Teilchen bis zur Messung in einer Superposition aller möglichen Zustände. Dieser Zustand kann als eine so in der Welt vorliegende "Überlagerung" aller möglichen Aufenthaltsorte des Elektrons gedeutet werden, man spricht bei dieser Auffassung von einer realistischen Wellenfunktion. Wenn das Quantenobjekt im Zuge einer Messung vom überlagerten Gesamtzustand |Ψ⟩ in einen möglichen und lokalisierten Eigenzustand |φi⟩ übergeht, dann kann man diesen Übergang kontinuierlich also zeitlich deuten. Oder man deutet ihn diskontinuierlich als ein instantan erfolgender Kollaps der Wellenfunktion deuten.
1.3. Nichtlokalität und Kausalität
Die Annahme eines Kollapses der Wellenfunktion hat zur Folge, dass wenn das Elektron an Ort A registriert wird, damit unmittelbar feststeht, dass es nicht am weit davon entfernten Ort B ist. Diese Eigenschaft wird als Quanten-Nichtlokalität bezeichnet. Die Quanten-Nichtlokalität widerspricht dem Prinzip der lokalen Wirkung, nach der eine Änderung in A keine Änderung im weit davon entferntem B bewirken kann. Albert Einstein betrachtete dieses Prinzip als eine notwendige Voraussetzung für die Existenz empirisch überprüfbarer Naturgesetze.[23]
Wenn zwei Elektronen überdies miteinander verschränkt werden, bewirkt dies eine statistische Korrelation der Messergebnisse zwischen beiden Elektronen. Selbst wenn sich die beiden Elektronen so weit von einander entfernt (an "zwei entgegengesetzten Enden des Universums") sind, dass entsprechend der Lichtkonstante keine physikalische Wirkung (Information) übertragen werden kann, bleibt diese "spukhafte Fernwirkung" bestehen. Es konnte allerdings gezeigt werden, dass auch innerhalb der Quantenmechanik keine überlichtschnelle Übertragung von Information möglich ist (siehe: No-signalling-Theorem). Dies legt die Existenz einer gegenseitigen Beeinflussung zwischen den Elektronen nahe, die nicht lokal über dem zwischenliegenden Raum oder nicht über Informationsaustausch vonstattengeht.
Die "spukhafte Fernwirkung" war einer der Gründe, weshalb Einstein die Quantenmechanik ablehnte. In dem berühmten, gemeinsam mit Boris Podolsky und Nathan Rosen entwickelten EPR-Gedankenexperiment versuchte er, unter der Prämisse der Lokalität nachzuweisen, dass die Quantenmechanik auf verborgenen Variablen beruht und keine vollständige Theorie sein kann.[24] Dieses Gedankenexperiment erwies sich in seiner ursprünglichen Formulierung als nicht praktisch durchführbar, jedoch gelang es John Stewart Bell den Kerngedanken von EPR in der experimentell überprüfbaren Form der Bellschen Ungleichung zu formulieren. Alle bislang vorliegenden experimentellen Untersuchungen deuten darauf hin, dass die Quantenmechanik nicht auf lokalen verborgenen Variablen beruht sondern vollständig ist.[25]
Daraus folgt wie gesehen nicht zwingend eine Verletzung der Lichtkonstante, sehr wohl aber eine Verletzung des Prinzips der lokalen Wirkung. Die Quantenmechanik wäre demnach tatsächlich nicht-lokal. Es gibt jedoch auch Interpretationen zur Bellschen Ungleichung, in denen das Prinzip der Lokalität beibehalten und das der Realität aufgegeben wird.[26] Die EPR-Debatte ist deshalb philosophisch gehaltvoll, weil sie uralte Frage nach der Realität von Eigenschaften, dem Holismus des Weltganzen und Wesen der Kausalität berührt.
1.4. Dekohärenz
Warum aber sind Makroobjekte immer real und lokal, wenn sie doch aus Quantenobjekten bestehen? Der Grund hierfür sind winzige Wechselwirkungen der Systeme mit der Umgebung, die unmittelbar zu dem Kollaps der Wellenfunktionen und Dekohärenzeffekten führen. Dekohärenzeffekt sind bei großen Objekten besonders stark, weshalb wir nie Tische oder Personen in einer Superposition beobachten. Auch Schrödingers Katze befindet sich nicht wirklich in einer Superposition zwischen "tot" und "lebendig", da sich so große Objekte kaum von der Außenwelt abschirmen lassen und stetig zB. mit Gasteilchen oder Strahlungen aus der Umgebung wechselwirken.
Das Phänomen der Dehohärenz lässt sich unmittelbar aus dem Formalismus der Quantenmechanik ableiten und experimentell nachüberprüfen. Er ist daher kein unmittelbarer Aspekt der IQM. Dennoch spielt er dort eine wesentliche Rolle, da er die Diskrepanz zwischen den ontologischen Aussagen der Interpretationen der Quantenmechanik und der Alltagserfahrung erklären kann.
2. Deutungen der Quantenmechanik
2.1. Ensemble-Interpretationen
Nach der Ensemble-Interpretation (auch: statistische Interpretation) repräsentiert die Wellenfunktion nicht nur ein reales Teilchen, sondern ein ganzes Ensemble. Sie wird oft als Minimalinterpretation verstanden, insofern sie dem mathematischen Formalismus genügt und ontologische Deutungen weitgehend auslässt. Jedoch adaptiert sie die Wellenfunktion (Bornsche Regel) nicht einfach nur, sondern deutet ihren Wahrscheinlichkeitsbegriff als relative Häufigkeit.
Diese semantische Deutung unterscheidet die Ensemble-Interpretation von einer Minimalinterpretation. Sie ist erstens philosophisch problematisch: Wenn ein bestimmter Messwert mit der Wahrscheinlichkeit 50% auftritt, dann werden etwa, aber eben nicht exakt die Hälfte aller Messungen diesen Wert ergeben. Zwar könnte man meinen, dass sich gemäß dem Gesetz der großen Zahlen die Messhäufigkeit an 50% annähert, aber auch das ist wieder nur äußert wahrscheinlich. Es ist durchaus möglich, dass auch bei einer Million Messungen kein einziges Mal unser Messwert auftritt. Die Reduktion von "Wahrscheinlichkeit" auf "relative Häufigkeit" funktioniert also nicht, da sich relative Häufigkeiten auch immer nur mit bestimmten Wahrscheinlichkeiten einstellen.
Zweitens ist diese Deutung physikalisch problematisch: Nach ihr handelt die Quantenmechanik nur von Ensembles, kann aber über einzelne Quarks oder Elektronen überhaupt nichts aussagen. Damit wäre sie epistemisch viel schlechter gestellt als alle anderen physikalischen Teildisziplinen, die sehr wohl beanspruchen, einzelne Systeme zu verstehen. Zudem müsste das auch bei einer Wiederholungsmessung gelten, bei der die Wahrscheinlichkeit eines bestimmten Messwerts bei 100% liegt. Selbst in diesem Fall könnte man nach der Ensemble-Interpretation nicht sagen, dass ein einzelnes Teilchen, sondern nur, dass das Ensemble aus Teilchen sicher diesen Messwert haben wird. Die Ensemble-Interpretation vertritt geradezu die Position, dass es quanten-ontologisch nur Ensembles und keine Teilchen gibt. Und das ist wenig überzeugend.
2.2. Kopenhagener Interpretation
Die Kopenhagener Interpretation galt lange Zeit als die "Standardinterpretation der Quantenmechanik". Sie wurde 1927 von Niels Bohr und Werner Heisenberg während ihrer Zusammenarbeit in Kopenhagen formuliert und später durch John von Neumann und Paul Dirac weiterentwickelt. Es handelt sich demnach genau genommen um einen Sammelbegriff ähnlicher Interpretationen, die aber einige charakteristische Gemeinsamkeiten aufweisen.
Gemäß der Kopenhagener Deutung ist der Wahrscheinlichkeitsbegriff der Bornschen Regel nicht Ausdruck der Unvollständigkeit der Theorie, sondern des ontologisch-indeterministischen Charakters quantenmechanischer Vorgänge. Aber auch diese Deutung ist philosophisch problematisch: Denn wenn die Nichtvorhersagbarkeit von quantenmechanischen Vorgängen doch auf epistemologischen und nicht auf ontologischen Gründen beruht, begeht Kopenhagen hier einen Kategorienfehler.
Anders als die Ensemble Interpretation spricht die Kopenhagener Interpretation dem einzelnen Teilchen Realität zu. Jedoch sind dessen Eigenschaften nicht unabhängig real, insofern sie erst durch das Messgerät festgelegt werden. Während ein Elektron – definiert über Ladung, Masse und Spin - also substantiell existiert, sind seine Impuls- oder Sprinprojektionswerte beispielsweise nur akzidentiell. Wie ich aber hier gezeigt habe, sind Elektronen allein über ihre "Substanz-Eigenschaften" weder zählbar noch wiedererkennbar, also weder Partikularen noch Individuen. Auch die bohrsche kopenhagener Quantenontologie scheint den Teilchen also keine individuelle Existenz zuzubilligen.
Eine Lösung dieses Problems besteht darin, mit Heisenberg über Bohr hinauszugehen und zwei zeitliche Dynamiken beim Messvorgang anzunehmen. Das verschärft aber wiederum das Messproblem: Wenn sich das Teilchen vor der Messung in einer Superposition befindet, müsste nach der Messung das neue Gesamtsystem Teilchen-Messgerät in einer Superposition sein. Was wir aber beobachten, ist ein unverschwommenes Messgerät und ein bestimmter Messwert.
Dieses Problem lässt sich offenbar nur lösen, indem man einen Heisenberg Cut zwischen Mikro- und Makroobjekt zieht. Wie die anhaltenden Diskussionen um eine angemessene Kritik an Schrödingers Katze zeigen, ist ein solcher Cut aber physikalisch problematisch, da es kein physikalisches Kriterium für die Unterscheidung von Mikro- und Makroobjekt gibt. Insbesondere geben die Gesetze der Physik und der Formalismus der Quantenmechanik eine solche Unterscheidung nicht her.[27] Auch die Dekohärenz kann diese Grenze nicht hinreichend erklären.[28]
2.3. De-Broglie-Bohm-Theorie
Die De-Broglie-Bohm-Theorie (auch: bohmsche Mechanik) geht davon aus, dass verborgene Variablen von der gegenwärtigen Theorie nicht erfasst werden und die vollständige Quantenmechanik deterministisch abläuft. Ein Teilchen bewegt sich also jederzeit entlang einer wohldefinierten Bahnkurve, die von der Wellenfunktion noch nicht erfasst wird und nur mit Hilfe der Bewegungsgleichung berechnet werden kann. Es ist deshalb erst durch die Wellenfunktion und seinen Ort vollständig bestimmt. Dadurch löst die bohmsche Mechanik das Messproblem, indem sie der Messung gar keine ausgezeichnete Rolle zuspricht. Der Ort des Teilchens war schon vor der Messung bestimmt und deshalb ist es auch nicht verwunderlich, dass das Messgerät nach der Messung nicht in eine Superposition übergeht.
Ein mathematisches Problem erwächst aus der Doppelrolle der Wellenfunktion: Diese legt sowohl die Teilchendynamik als auch die Gleichgewichtsverteilung fest. Zudem ist die Welt nach der De-Broglie-Bohm-Theorie mit zahlreichen "leeren" Wellenfunktionen bevölkert, die keine Teilchenbahnen enthalten und aufgrund von Dekohärenz keinen Einfluss auf die Teilchendynamik haben. Einige kritisieren das Aufkommen von leeren Wellenfunktionen als mathematisch unelegant, andere sehen sie als bemerkenswerte Neuerung der Naturbeschreibung.
Der Haupteinwand gegen die De-Broglie-Bohm-Theorie berührt aber ihre relativistische Verallgemeinbarkeit (siehe: Quantengravitation). Die DBBT ist nicht-lokal, das heißt sie verknüpft Teilchen in beliebiger Entfernung. Dies scheint dem Postulat der Lichtkonstante in der Relativitätstheorie zu widersprechen. Auch die Quantengleichgewichtsbedingung und die Forderung der der Lorenztkovarianz stehen im Widerspruch zueinander.[29] Die Quantengleichgewichtsverteilung zeichnet nämlich das Bezugssystem aus, in dem diese Verteilung vorliegt. Nach dem einsteinschen Relativitätsprinzip sind aber alle Inertialsysteme gleich.
2.4. Viele-Welten-Interpretation
Die Viele-Welten-Interpretation geht auf Hugh Everett III. zurück. Nach ihr spaltet sich das gesamte Universum (inklusive dem Beobachter) andauernd in so viele Paralleluniversen auf, wie es gemäß der universalen Wellenfunktion mögliche Messergebnisse gibt. Dies löst das Messproblem, da nicht nur ein bestimmtes, sondern jedes Ergebnis bzw. Ereignis mit einer Wahrscheinlichkeit größer Null in einem Universum auch tatsächlich realisiert ist. Dementsprechend kollabiert die Wellenfunktion auch niemals und gibt auch nicht die absoluten Wahrscheinlichkeiten für das Auftreten potentiell-möglicher Messergebnisse an.
Der Beobachter bemerkt die ständige Aufspaltung in Myriaden Parallelwelten nicht, da er sich immer nur in einer befindet. Welten, die sich in makroskopischer Größenordnung voneinander unterscheiden, entwickeln sich aufgrund von Dekohärenzeffekten fast unabhängig voneinander. Das einzige nachweisbare Indiz der Existenz von anderen Welten sind Interferenzeffekte, die sich beobachten lassen, wenn sich die Welten nur auf mikroskopischer Ebene unterscheiden.
Die Viele-Welten-Interpretation ist somit falsifizierbar. Dennoch wird ihr zurecht eine überbordente Ontologie vorgeworfen, die das Sparsamkeitsprinzip verletzt. Dem kann man entgegnen, dass die VWI in der Anwendung des wissenschaftlichen Realismus einfach weiter geht als andere Theorien. Die Viele-Welten sind ja kein unabhängiges Postulat, sondern folgen aus der konsequent realistischen Deutung der Schrödingergleichung, also aus einer empirisch bewährten Formel. Dies verkürze und vereinfache die Axiomatik der Quantenmechanik und sei somit ganz im Sinne von Ockhams Razor.
Das schwerwiegendste Argument gegen die VWI betrifft das Determinismusproblem. Gemäß der VWI wird bei einer Messung jedes mögliche Ergebnis tatsächlich realisiert. Das wirft die Frage auf, inwiefern es sinnvoll ist, von Wahrscheinlichkeiten zu sprechen. Kritiker meinen, dass die VWI einen "übernatürlichen Beobachter" erfordere, um die Wahrscheinlichkeitsinterpretation von Messungen plausibel zu machen. Und selbst dann wäre noch nicht geklärt, warum alltägliche Beobachter die QM als indeterminiert erleben, wenn alle Welten doch determiniert sind.[30] Vertreter der VWI pochen hier auf eine strikte Unterscheidung von Außen- und Innenperspektive und argumentieren, dass für einen Beobachter aus der Innenperspektive ein Ereignis trotz der deterministischen Entwicklung eines Zustandes gemäß der Schrödingergleichung zufällig wirken kann.[31]
2.5. Dynamischer-Kollaps-Theorien
Die Grundidee der dynamischer-Kollaps-Theorien ist die Lösung des Messproblems durch die Annahme, dass die Wellenfunktion zu zufälligen Zeitpunkten kollabiert.[32][33] Zur Beschreibung der Kollaps-Vorgänge wird die Schrödingergleichung um Terme erweitert, die so gewählt sind, dass die Lokalisierungsrate bei isolierten mikroskopischen Systemen praktisch vernachlässigbar, bei makroskopischen Systemen hingegen dominant ist. Die Theorie erklärt damit, weshalb die aus der Schrödingergleichung resultierenden und nicht-lokalen Überlagerungszustände nur bei mikroskopischen Systemen auftreten, während Tische und Personen immer lokalisiert sind.
Da sich die Grundgleichungen der dynamischer-Kollaps-Theorien von der Schrödingergleichung unterscheiden, handelt es sich bei diesen Theorien strenggenommen nicht um Interpretationen der Quantenmechanik, sondern um alternative Theorien, deren Abweichungen zur Quantenmechanik im Prinzip experimentell überprüfbar sind. Allerdings erfordert der Nachweis dieser Abweichungen die kontrollierte Erzeugung makroskopischer Quantenzustände in einer Größenordnung, die gegenwärtig nicht realisierbar ist.[34]
Die älteste vollständig ausgearbeitete dynamischer-Kollaps-Theorie ist die so genannte GRW-Theorie (nach ihren Autoren Ghirardi, Rimini und Weber).[35] Auch GRW beansprucht eine einheitliche Dynamik für Mikro- und Makrosysteme zu geben, so dass die grundlegende Wellenfunktion in aller Regel keine eines einzelnen Quantensystems, sondern eine von sehr, sehr vielen Teilchen ist.
Der Ortsraum, der solche Systeme beschreibt, ist daher kein 3-dimensionaler Anschauungsraum, sondern vielmehr ein 3N-dimensionaler "Konfigurationsraum". Dieser Raum verdreifacht mit jedem hinzukommenden Teilchen seine Dimensionsanzahl und ist dementsprechend unanschaulich. Dennoch wird ernsthaft vertreten, dass er physikalisch real ist und unsere Anschauung eines bloß drei-dimensionalen Raums trüge.[36] Demgegenüber wurde beispielsweise von John Bell behauptet, dass der Konfigurationsraum nur ein abstrakt-mathematischer und vom realen Raum zu unterscheiden sei.[37]
2.6. Quanten-Bayesianismus
Der Quanten-Bayesianismus zählt zu den Informationsbasierten Deutungen. Mit ihm wurde im letzten Jahrzehnt die erste konsequent subjektivistische Interpretation der Quantenmechanik vorgelegt. Nach ihr beziehen sich die durch die Wellenfunktion ausgedrückten Wahrscheinlichkeiten nicht auf eine objektive Unbestimmtheit, sondern auf unser beschränktes Wissen. Mit der Messung verändert sich dementsprechend auch nicht die Welt (es kommt zu keinem Kollaps), sondern unser Wissen über sie. Die Wahrscheinlichkeiten der Messergebnisse werden dabei auf subjektivistische bayesianische Wahrscheinlichkeiten zurückgeführt.[38][39][40]
Der QB enthält sowohl realistische als auch anti-realistische Elemente:[41] Quantenobjekte wie Elektronen, Neutrinos und Quarks werden als real angenommen. Quantensysteme besitzen hingegen nur die dispositionellen Eigenschaften, im Falle einer Wechselwirkung bestimmte Ereignisse zu verursachen. Der Verlauf dieser Ereignisse ist durch kein physikalisches Gesetz bestimmt, selbst die Gültigkeit stochastischer Gesetzmäßigkeiten auf mikroskopischer Ebene wird in dieser Interpretation verneint.[42] Als Vorteil des Quanten-Bayesianismus führen seine Anhänger an, dass viele der gängigen (scheinbaren) Paradoxien der Quantenmechanik, wie z. B. Schrödingers Katze, im Rahmen dieser Interpretation vermieden werden können, da die meisten dieser Paradoxien auf einer objektiven Interpretation des quantenmechanischen Zustandes basieren.[43]
Weiterhin vertreten sie in der (unabhängig von der Quantenmechanik existierenden) Kontroverse um die Interpretation von "Wahrscheinlichkeit" den Bayesschen Standpunkt, dass nur eine subjektivistische Wahrscheinlichkeits-interpretation ohne logische Inkonsistenzen formulierbar sei. Andere Autoren, wie der Physiker G. Jaeger oder der Philosoph C. Timpson, kritisieren, dass der Quanten-Bayesianismus ein Defizit an Erklärungsvermögen aufweise. Die Zielsetzung von Physik sei die Beschreibung und Erklärung physikalischer Systeme, nicht die Beschreibung der Einschätzungen von Beobachtern.[44][45]
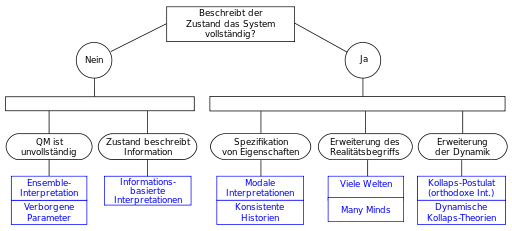
Urheber der Grafik: Belsazar (Creative Commons 3.0)
Einzelnachweise
[1] C. A. Fuchs, A. Peres: Quantum Theory needs no "Interpretation"
[2] E. Dennis, T. Norsen: Quantum Theory: Interpretation Cannot be avoided. arxiv:quant-ph/0408178
[3] Die in den Zellen der Tabelle gezeigten Werte sind nicht unumstritten, denn die genauen Bedeutungen einiger der beteiligten Konzepte sind unklar und stehen selbst im Mittelpunkt der Kontroverse eine Interpretation. Für eine andere Tabelle, die Interpretationen der Quantentheorie vergleicht, siehe: Lombardi, Olimpia,, Fortin, Sebastian, 1979-, Holik, Federico,, López, Cristian,: What is quantum information?, ISBN 9781107142114, OCLC 965759965.
[4] Eine sperrigere, indes präzisere Bezeichnung wäre "Kontrafaktische Bestimmtheit".
[5] Nach Bohr hat das Konzept eines physikalischen Zustands, der unabhängig von den Bedingungen seiner experimentellen Beobachtung ist, keine klar definierte Bedeutung. Nach Heisenberg stellt die Wellenfunktion eine Wahrscheinlichkeit dar, nicht aber eine objektive Realität in Raum und Zeit.
[6] Gemäß der
Kopenhagener Interpretation bricht die Wellenfunktion zusammen, wenn eine Messung durchgeführt wird. Vgl. Abschnitt "Realismus und Kollaps der Wellenfunktion".
[7] Beide Teilchen und Führungswellenfunktion sind real.
[8] Eindeutige Partikelhistorie, aber mehrere Wellenhistorien.
[9] Die Art von Nichtlokalität, die von der Theorie verlangt wird, um die Bell-Ungleichungen zu verletzen, ist schwächer als die in EPR angenommene. Insbesondere ist diese Art von Nicht-Lokalität kompatibel mit keinem Signalisierungstheorem und Lorentz-Invarianz!
[10] Die Quantenlogik ist in ihrer Anwendbarkeit aber begrenzter als kohärente Historien.
[11] Der Kollaps des Zustandsvektors wird als Abschluss der Transaktion zwischen Emitter und Absorber interpretiert.
[12] Die
transaktionale Interpretation ist explizit nicht-lokal.
[13] Jede physische Interaktion wird als ein Kollaps-Ereignis relativ zu den beteiligten Systemen behandelt, nicht nur makroskopische oder bewusste Beobachter.
[14] Der Zustand des Systems ist beobachtungsabhängig, d. H. der Zustand ist spezifisch für den Referenzrahmen des Beobachters.
[15] Die
Annahme der intrinsischen Periodizität ist ein Element der Nicht-Lokalität, die mit der Relativität konsistent ist, da die Periodizität kausal variiert.
[16] Eine Wellenfunktion kodiert lediglich die Erwartungen eines Agenten für zukünftige Erfahrungen. Es ist nicht mehr real als eine Wahrscheinlichkeitsverteilung ist in der Bajian (Bajaan
Wahrscheinlichkeit).
[17] Obwohl QBism diese Terminologie vermeiden würde. Eine Veränderung der Wellenfunktion, die ein Agent einem System als Ergebnis einer Erfahrung zuschreibt, stellt eine Veränderung
seiner Überzeugungen über weitere Erfahrungen dar, die sie möglicherweise haben.
[18] Beobachter oder, richtiger, Teilnehmer sind für den Formalismus genauso wichtig wie die Systeme, mit denen
sie interagieren.
[19] Der Standpunkt, dass die klassische Mechanik wirklich deterministisch ist und Ungenauigkeiten auf die Unfähigkeit des Experimentators zurückzuführen
sind, ist nicht vollkommen unumstritten. Entgegengesetzter Ansicht war beispielsweise Karl Popper. Karl Popper: Indeterminism, S. 117–133 und Karl Popper: Indeterminism in Quantum Physics and in Classical Physics II, S.
173–195.
[20] Eine Ausnahme bilden vielleicht die in der Allgemeinen Relativitätstheorie aufkommenden Singularitäten.
[21] Gerhard Schurz: Wahrscheinlichkeit, S. 56
[22] A. Zeilinger spricht beispielsweise von einem "objektivem Zufall". Werner Heisenberg den Begriff der "Potentia". Auch Poppers Propensitäten-Interpretation liegt ein ähnliches Konzept von Wahrscheinlichkeit zugrunde.
[23] Albert Einstein: Quantenmechanik und Wirklichkeit, S. 320–324.
[24] EPR: Can quantum-mechanical description of physical reality be considered complete?, S. 777–780
[25] Alain Aspect: Experimental Tests of Realistic Local Theories via Bell’s Theorem, S. 460
[26] S. Gröblacher et al.: An experimental test of non-local realism, S. 871
[27] David Albert: Quantum Mechanics and Experience, S. 91: Man kann mit dem Formalismus der Quantenmechanik sogar mathematisch zeigen, dass unter der Voraussetzung, dass ein (realer) Kollaps stattfindet, man prinzipiell nicht feststellen kann, wann er stattfindet, also wo der (objektive) Schnitt zwischen Mikro- und Makrosystem liegt.
[28] Cord Friebe: Philosophie der Quantenphysik, S. 60
[29] K. Berndl, D. Dürr, S. Goldstein, N. Zanghe: Nonlocality, Lorentz invariance, and Bohmian quantum theory, S. 2062–2073
[30] Adrian Kent: Against Many-Worlds Interpretations, S. 1745–1762
[31] Max Tegmark: The Interpretation of Quantum Mechanics: Many Worlds or many words?
[32] G. Ghirardi: Collapse Theories.
[33] A. Bassi, G. Ghirardi: Dynamical reduction models.
[34] D. Kleckner: Creating and Verifying a Quantum Superposition in a Micro-optomechanical System.
[35] GRW: Unified dynamics for microscopic and macroscopic systems, S. 470–491
[36] John Belll: Are there Quantum Jumps, 204 f.
[37] David Albert: Quantum Mechanics and Experience, S. 92 f.
[38] G. Jaeger: Entanglement, S. 188 und S. 234 ff.
[39] A. Duwell: Quantum information does exist, S. 195.
[40] C. Timpson: Information, Immaterialism, Instrumentalism
[41] C. Timpson: Quantum Bayesianism, Kap. 4.1.
[42] ebd.
[43] C. Timpson: Quantum Bayesianism, Kap. 2.1.
[44] "The question is what physical insight into the quantum world is gained from this interpretation other than, to borrow a phrase from Einstein, a “gentle pillow for the true believer in the information age”?", in: G. Jaeger, Entanglement, Information, and the Interpretation of Quantum Mechanics, S. 179.
Siehe auch
Stand: 2018
 Philoclopedia
Philoclopedia
tsSLAueP (Mittwoch, 15 November 2023 20:11)
1
tsSLAueP (Mittwoch, 15 November 2023 17:17)
1
Philoclopedia (Freitag, 05 November 2021 23:10)
http://philsci-archive.pitt.edu/9550/1/Quantumdefence_rev.pdf
Philoclopedia (Samstag, 03 Juli 2021 12:01)
https://www.academia.edu/13149824/On_the_Importance_of_Interpretation_in_Quantum_Physics_A_Reply_to_Elise_Crull?email_work_card=view-paper
Philoclopedia (Samstag, 03 April 2021 23:57)
https://oxford.universitypressscholarship.com/view/10.1093/acprof:oso/9780199535408.001.0001/acprof-9780199535408?rskey=LDHd1s&result=87
Nibba (Freitag, 20 September 2019 09:22)
yeet
Torsten Krieg (Donnerstag, 12 September 2019 10:44)
Der in der Quantenmechanik herrschende Zufall erhält in folgender Hypothese eine physikalische Begründung:
https://www.quanten-krimi.de
WissensWert (Samstag, 13 Oktober 2018 04:29)
Die Rolle des Beobachters
Eine Messung beschreibt die Wechselwirkung zwischen Messobjekt und Messapparatur. Laut dem Ideal des losgelösten Beobachters[20] ist der Einfluss der MA auf das MO vernachlässigbar, beide werden daher als distinkteEntitäten aufgefasst. Dieses Ideal ist zwar auch in der klassischen Physik nichtvollständig erreicht, das jedoch nicht aus grundsätzlichen, sondern nur aus praktischen Gründen. Spätestens durch die spezielle Relativitätstheorie wird es verletzt, da hier die räumliche und zeitliche Abstände sowie die Gleichzeitigkeit von Ereignissen von der relativen Bewegung des Beobachters abhängen.
In der Quantenmechanik wird das Ideal des losgelösten Beobachters auf ganz besondere Weise verletzt. Generell ist jede Wechselwirkung des Objektsystems mit der Messvorrichtung mit Dekohärenzprozessen verbunden, deren Auswirkungen nicht als "vernachlässigbar klein" betrachtet werden können. Schon dadurch scheint ein quantenmechanisches Messergebnis beobachterabhängig zu sein. Dieser Eindruck wird durch das im nächsten Abschnitt beschriebene Messproblem vielfach verstärkt. In vielen Fällen (beispielsweise beim Nachweis eines Photons durch einen Detektor) kommt es bei der Quantenmessung sogar zu einer Eliminierung des Messobjekts (Teilchenvernichtung).
WissensWert (Mittwoch, 01 August 2018 03:19)
https://www.thur.de/philo/project/qt.htm