Fermion
Fermionen (auch: Fermi-Teilchen, benannt nach dem Physiker Enrico Fermi) sind Teilchen mit halbzahligem Spin (sprich: h/2, 3h/2 etc.). Anschaulich gesprochen sind Fermionen folglich diejenigen Teilchen, aus denen die uns umgebende Materie aufbaut ist ("Materieteilchen") und ihr Counterpart sind die Bosonen, die einen ganzzahligen Spin besitzen und zwischen den Fermionen Kräfte vermitteln ("Kraftteilchen").
# Fermionen sind Mini-Materiebausteine.
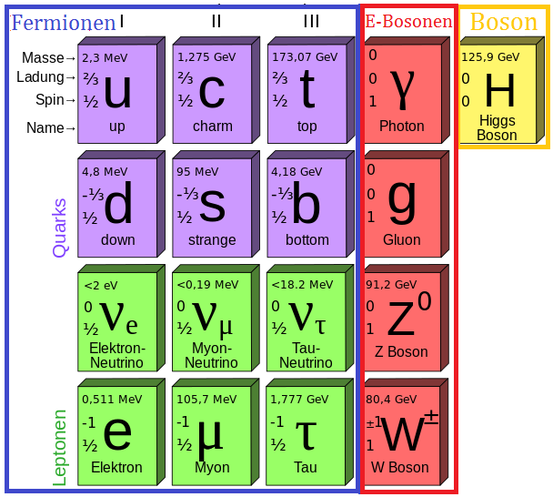
Fermionen und Bosonen
In der Physik ist man bestrebt, auch die komplizierten Vorgänge in der Welt auf möglichst einfache Grundstrukturen zurückzuführen. Die Erkenntnisse der Quantenmechanik haben ergeben, dass sowohl die Materie, als auch die Kräfte auf Entitäten zurückführbar sind, die der Natur zugrunde liegen und in der Physik Teilchen genannt werden.
Teilchen sind jedoch nicht gleich Teilchen: Das Spin-Statistik-Theorem zieht einen Trennstrich zwischen Teilchen mit halbzahligen Spin, den Materieteilchen, und Teilchen mit ganzzahligem Spin, den Kraftteilchen.
Materieteilchen, also Fermionen, können in der Quantentheorie sowohl als Teilchen, als auch als Wellen beschrieben werden. Die Wellenfunktion eines Fermions ist bezüglich des Austausches zweier Teilchen antisymmetrisch, d.h. sie wechselt bei einem solchen Austausch ihr Vorzeichen. Ganz anders die Bosonen, denen in dieser Hinsicht symmetrische Wellenfunktionen zukommen.
Eine Folge der unterschiedlichen (Anti-)Symmetrien der bosonischen und fermionischen Wellenfunktionen ist, dass Fermionen dem sogenannten Pauli-Prinzip unterliegen, Bosonen hingegen nicht. Nach dem Pauli-Prinzip können sich zwei oder mehrere Fermionen niemals gleichzeitig im gleichen Quantenzustand befinden, d.h. nie in ihren sämtlichen Quantenzahlen übereinstimmen.
Dieser Sachverhalt ist von grundlegender Wichtigkeit für den Aufbau unserer materiellen Welt: Offensichtlich wird Materie durch eine Vielzahl an Teilchen konstituiert, die sich gegenseitig "abstoßen" und diese "Abstoßung" ist es, die der Materie als Ganzem erst ihre Ausdehnung und Festigkeit verleiht.
Fermionen im Standardmodell
Zu den Fermionen gehören:
· Elementarteilchen: Leptonen (z.B. Elektron und Myon-Neutrino) und Quarks (z.B. up-Quark und bottom-Quark).
· Zusammengesetzte, d.h. nicht-elementare Teilchen: u.a. Baryonen, wie das Protonund das Neutron, die sich aus einer ungeraden Anzahl von Quarks zusammensetzen.
Die folgende Tabelle gibt eine Übersicht über die elementaren Fermionen:
|
Elementare Fermionen |
|
Gruppe: |
Leptonen |
Quarks |
||
|
Ladung: |
-1 |
0 |
-1/3 |
+2/3 |
|
1. |
Elektronen |
Elektronen- |
down-Quarks |
up-Quarks |
|
2. |
Myonen |
Myonen- |
strange-Quarks |
charm-Quarks |
|
3. |
Tauonen |
Tauonen- |
bottom-Quarks |
top-Quarks |
Von den beiden elementaren Fermionentypen, Leptonen und Quarks, gibt es je zwei Ladungszustände: einfach negativ und neutral für Leptonen und minus ein Drittel negativ und zwei Drittel positiv für Quarks. Überdies kommen Leptonen und Quarks in drei Generationen vor, wobei ein Elementarteilchen höherer Generation immer schwerer ist, als ein Elementarteilchen niederer Generationsstufe. Ansonsten weißen "Generationspartner" wie etwa das Elektron und das Tauon (nahezu) exakt dieselben Eigenschaften auf. Warum das alles so ist, weiß man nicht.
"Normale" Materie besteht übrigens nur aus Teilchen erster Generation: Die Atomhüllen der normalen Materie werden von Elektronen gebildet und ihr Atomkern von "first-generation"-Quarks, die sich zu Baryonen zusammensetzt haben. Die Teilchen höherer Generationen sind zu instabil, um "auf freier Wildbahn zu überleben". Sie können nur künstlich erzeugt werden und zerfallen selbst danach wieder blitzschnell in Teilchen aus der ersten Generation.
Verweise
-
#Fermi-Dirac-Statistik
-
#Majorana-Fermion ist die Bezeichnung für
ein Teilchen, das identisch mit seinem zugehörigen Antiteilchen ist. Diese Definition impliziert, dass kein
Majorana-Fermion keine elektrische
Ladung ungleich Null besitzen
darf.
-
#Weyl-Fermion
-
Algebra: Es gibt eine Algebra,
die CAR-Algebra, die aufgrund ihrer engen Verwandtschaft zu den kanonischen
Antivertauschungsrelationen, gelegentlich auch Fermionenalgebra genannt wird.
-
Anyon ist ein dritter
Teilchentyp, der sich weder den Fermionen, noch den Bosonen zuordnen lässt. Das exotischeAnyon trägt nämlich weder einen halbzahligen (Fermion), noch einen ganzzahligen Spin (Boson), es genügt einer ganz eigenen Quantenstatistik. Jedoch kommt es ausschließlich
in sehr dünnen Schichten vor, in "zweidimensionalen Systemen". Ein Elementarteilchen in allen drei Raumdimensionenmuss dann wieder entweder ein Fermion oder ein
Boson sein.
-
Atomismus: Der antike
Philosoph Demokrit vertrat die These, dass die Dinge in der Welt nur scheinbar farblich seienund auch nicht wirklich süß oder bitter schmecken würden. In Wirklichkeit, so Demokrit, gäbe es nur den Raum und
Atome in selbem, aus denen alle Gegenstände aufgebaut seien. Atome waren für Demokrit
nicht weiter teilbare Objekte, eine Art "kleinste Bausteine der materiellen Realität" also, eine Vorstellung, die der modernen von Fermionen erstaunlich nahe kommt. Es kann Verwirrung
stiften, dass das Wort "Atom" auch im modernen Sprachgebrauch vorkommt, dort aber ein Objekt bezeichnet, das sehr wohl weiter teilbar ist. Verwirren kann vielleicht auch, dass sich Demokrit
seine Atome mit Haken und Ösen dachte, mit denen sie sich untereinander zu größeren Einheiten verbinden können sollten. Hier hat er offensichtlich eine Eigenschaft größerer Objekte auf
kleinere übertragen und ich hätte ihn nur zu gerne gefragt, wie er mit dem Widerspruch umgehen möchte, dass Haken und Ösen (nach der klassischen Vorstellung) doch selbst wieder eigenständige
Objekte sind, die doch vom Rest des Körpers abgetrennt werden können, aber gleichzeitig ein Teil der unteilbaren Atome sein sollen. Die hiermit implizit formulierte Frage, ob es überhaupt kleinste Teilchen geben kann, wenn man doch alle im Raum ausgedehnte Teilchen, zumindest im Prinzip, wieder "in der Mitte entzweischlagen" können müsste, umschifft
die heutige Physik ganz geschickt, in dem sie den wirklich unteilbaren Objekten eine Ausdehnung von Null postuliert. Frei nach dem Motto: "Wo keine Ausdehnung vorhanden ist, kann auch
nirgends zwischengeschlagen werden." Das bedeutet im Umkehrschluss aber auch, dass sobald es gelingt, Elektronen oder Myonen eine räumliche Ausdehnung nachzuweisen, diese nicht elementar sein
können, sondern aus noch kleineren Teilchen zusammengesetzt sein müssen. Dieser Regress auf der Suche nach den "punktförmigen Elementarteilchen" kann freilich nicht ewig weitergehen: Viele
Interaktionen zwischen den Teilchen werden mathematisch als Funktionen ihres Abstandes beschrieben, und Teilchen, die selbst keine Ausdehnung besitzen, könnten sich theoretisch beliebig nahe
kommen, aber bei einer Entfernung von Null zwischen zwei Teilchen erhält man mathematisch unsinnige Ergebnisse. Es scheint auf dem ersten Blick, als habe die Annahme der Teilchen ohne
Ausdehnung uns vor einem Problem, das mit dem kleinsten Teilchen, gerettet, und uns sofort wieder in ein neues geritten: dass der beliebig nahe zueinander stehenden Elementarteilchen. Aber
auch hieraus schlägt uns die heutige Physik einen Ausweg: Laut der Heisenberschen Unschärferelation ist der
Aufenthaltsort eines jeden Teilchens nicht beliebig exakt bestimmbar, wodurch es zwar selbst keine Ausdehnung hat, sein Aufenthaltsort aber schon. Einen weiteren "Ausweg" kann die
Stringtheorie ebnen: Nach ihr setzen sich Teilchen und sowieso alles Materielle aus elementaren Strings zusammen, die wenigstens in einer Dimension eine Ausdehnung
besitzen. Die Zukunft wird zeigen, ob einer dieser beiden Ansätze das (mathematische) Problem der unendlich nahen Elementarteilchen zu lösen vermag. Ein anderes bleibt aber sicher bestehen:
Wie können Teilchen, die sich selbst gar nicht in den Raum hinein ausdehnen, in jenen leeren Raum hineinwirken?
-
Letztbegründung: Philosophisch interessant ist die Suche nach den kleinsten Teilchen, weil
sie uns geradewegs zum Problem mit den Letztbegründungen führt: Hat man für A den Grund B ausfindig gemacht, lässt sich immer noch nachschieben, was den der Grund C für B ist usw.? Genauso
verhält es sich mit den kleinsten Teilchen: Wenn man etwas über das vermutlich kleinste Teilchen A aussagen möchte, lässt sich eigentlich immer die Frage anhängen, woher und woraus dieses
etwas ist, wenn nicht aus einem noch kleineren B? Ironischerweise wäre die Annahme, zu der solche Gedanken führen können, dass es keine Letztbegründungen geben kann, selbst eine Art
Letztbegründung. Sie wäre somit selbstwidersprüchlich.
-
Chemie: Ohne das Pauli-Prinzip gäbe es, verkürzt gesagt, keine Chemie. Denn
dann befänden alle Elektronen immer in ihrem Grundzustand und Dinge wie Elektronenschalen wären ohne Bedeutung. Chemische Reaktionen sind aber nichts weiter als Vorgänge in den
Elektronenschalen. Also: Ohne Pauli-Prinzip keine Elektronenschalen, ohne Elektronenschalen keine Chemie / keine chemischen Reaktionen.
-
Elektron: Angewendet auf die
Elektronen, die um ein Atom herumschwirren, besagt das Pauli-Prinzip, dass nicht alle Elektronen in denselben Grundzustand fallen können, sondern paarweise die verschiedenen Atomorbitale
eines Atoms auffüllen. Erst durch diese Eigenschaft erklärt sich der systematische Aufbau des Periodensystems der chemischen Elemente.
-
Quarks: Alle Quarks - und alle aus Quarks bestehenden, nicht-elementar-Teilchen,
wie die aus drei Quarks zusammengesetzten Baryonen (z.B. Neutronen und Protonen) zählen zu den Fermionen. Aber nicht alle Fermionen sind Quarks, es gibt neben den Quarks noch eine zweite,
fermionische Teilchenklasse: die Leptonen.
-
Spin: Eine sonderbare Eigenschaft der Fermionen mit dem Spin ½ ist, dass man sie
um 720° "drehen" muss, bis sie wieder in ihrem Ausgangszustand sind. Nach einer 360°-Drehung ändert sich nur das Vorzeichen ihrer Wellenfunktion und man sieht nicht dasselbe Fermion, wie vor
der einmaligen Drehung. Hier lässt sich eine Analogie zum Stundenzeiger auf einem Ziffernblatt herstellen: Erst nach einer Drehung des Stundenzeigers um 720°, also zweimal drum herum, zeigt
er wieder die gleiche Tageszeit an.
- Supersymmetrie: Gibt es vielleicht mehr Fermionen, als wir bzw. unser Standardmodell weiß? Im um die Supersymmetrie erweiterten Modell der Elementarteilchen existieren weitere elementare Fermionen, die im (nicht super-symmetrischen) Standardmodell nicht vorkommen. Wenn es nach der (bisher nicht experimentell bestätigten!) Supersymmetrie geht, dann kommt auf jedes Boson ein supersymmetrisches Femion-Partnerteilchen, ein so genanntes Bosino, so dass sich der Spin jeweils um ±1/2 unterscheidet. Die Superpartner der Bosonen werden ebenfalls durch die Endung –ino im Namen gekennzeichnet, z.B.: Photino, Gluino, Gravitino).
Stand: 2015
 Philoclopedia
Philoclopedia
ghovjnjv (Donnerstag, 08 September 2022 13:05)
1