Stringtheorie
1. Strings
Als zentraler und namensgebender Ausgangspunkt postuliert die Stringtheorie sogenannte Strings (englisch für Fäden, Saiten). Strings sind eindimensionale Energieobjekte und die elementaren Freiheitsgrade der Stringtheorie. Daher auch die Entlehnung des Wortes an die scheinbar eindimensionalen Fäden. Gegenüber der konventionellen ist diese Ansicht nun diametral verschieden. Denn das Standardmodell der Teilchenphysik geht von nulldimensionalen Objekten im Sinne von Punkten als fundamentale Bausteine der Welt aus. Quarks und Elektronen seien quasi die letzte der Matrjoschka-Puppen, die sich nicht mehr weiter auseinandernehmen lassen. Auch neue Experimentaldaten legen diese Vermutung nahe. Die Stringtheorie indes sieht nun in Objekten mit eindimensionaler räumlicher Ausdehnung die kleinste aller Matrjoschka-Puppen. Die Bezeichnung der Auffassung, etwas bestehe aus nicht weiter reduzierbaren Elementen, lautet Atomismus (a-tomos, nicht teilbar). Die Stringtheorie widerspricht dem radikalen Atomismus, da Strings mit räumlicher Ausdehnung prinzipiell noch teilbar sein müssten.

Die Längenskala eines gewöhnlichen Strings müsste in der Größenordnung der Plancklänge liegen. Gegenüber einem Atom ist dies noch einmal ein paar Größenordnungen kleiner, als das Atom gegenüber einem Menschen. Also unheimlich klein. Und somit weit außerhalb des derzeit für uns empirisch Messbaren. Im absoluten Ausnahmefall, etwa bei besonderen Spannungen, könnte ein String aber auch wesentlich größer werden. Für gewöhnlich sind Strings jedoch so klein, dass sie sich in unseren Laboratorien nicht von nulldimensionalen Teilchen unterscheiden lassen. Dies macht eine Falsifikation der Stringtheorie problematisch.
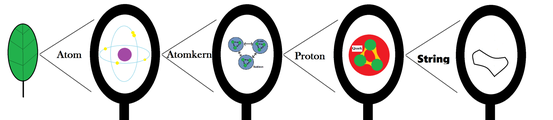
Strings können offen und geschlossen sein. Ein geschlossener String besitzt keine Endpunkte und ist daher topologisch äquivalent zu einem Kreis. Man kann ihn sich in Schleifenform vorstellen. Den offenen String kann man sich mithilfe seines Namensvetters im Englischen, der Saite, in Linienform vorstellen. Er ist topologisch zu einer Strecke.
Nach der speziellen Relativitätstheorie überstreicht ein dreidimensionales Objekt entlang der Raumzeit eine eindimensionale Weltlinie. Dieses Konzept lässt sich auf andersdimensionale Objekte extrapolieren. Demnach besitzt ein eindimensionaler String eine zweidimensionale Weltfläche, eine zweidimensionale Fläche als physikalisches Objekt entspricht einem Weltvolumen, usw. Eine weitere Konsequenz aus der speziellen Relativitätstheorie ist die Äquivalenz von Masse und Energie. Ihr verdanken wir es, dass aus den Energiefäden feste Materie werden kann. Denn sie besagt, dass Masse und Energie in Relation zum konstanten Faktor Lichtgeschwindigkeit zum Quadrat dasselbe seien.
Teilchenarten
Es drängt sich jetzt natürlich die Frage auf, wie die Stringtheorie die Vielfalt an Elementarteilchen mit nur einem einzigen String erklären will? Wir wissen bereits, dass die Energie eines Strings einer bestimmten Masse entspricht. Diese physikalischen Größen lassen sich wie bei Meter und Dezimeter mit dem Faktor zehn umrechnen. Auf den großen konstanten Faktor c² hin wohnt selbst dem massearmen String beachtlich viel Energie inne. Nun stellen Sie sich vor, man hebt den String aka Faden vor die spielende Anlage eines riesigen Technokonzerts. Der Faden wird anfangen zu schwingen. Stärker mit zunehmender Leistung aus den Boxen. Und auch Strings schwingen mit zunehmender Energie immer mehr.

- Hauptteil
# der String als elementarstes Elementarteilchen. Als wahres Atom.
Die unterschiedlichen Schwingungsarten bezeichnet mal als Moden. Die unterschiedlichen Vibrationsmoden der Strings entsprechen dabei den verschiedenen Elementarteilchen des Standardmodells. Jede der vielen möglichen Schwingungen ist also charakteristisch für die Eigenschaften eines bestimmten Teilchens. Alle Teilchen sind jedoch nur unterschiedlich schwingende Strings. Resümierend lässt sich festhalten, dass die Modalität der Moden die Teilchenart determiniert.
# „down-Quark-String“
Spin, elektrische Ladung, Masse und all die anderen Merkmale, die ein up-Quark von einem Elektron unterscheiden, sind folglich nur Erscheinungsformen von Schwingmustern. Diese sind selbst mit mathematischen Vorkenntnissen schwer zu entschlüsseln. Ein relativ unkomplizierter Mechanismus steckt hinter der Teilchenmasse. Die Stärke der Schwingung definiert die Teilchenmasse. Ein schwereres Teilchen ist die Repräsentation eines heftiger schwingenden Strings. Ab einem bestimmten Punkt schlägt eine weitere Energiezufuhr jedoch in eine Längenzunahme des Strings um. Unsere Möglichkeiten übersteigt ein solches Vorhaben zwar bei Weitem, aber eventuell brachte der Urknall aufgrund dieses Umstandes mit seiner enormen Energiedichte makroskopische Strings hervor.
# quantisierte Stringmassen.
Die aus dem Schwingungsprozess ausgedrückte Energie ist immer ein ganzzahliges Vielfaches der Planck-Masse, die wiederrum proportional zur Stringspannung ist. Die möglichen Stringmassen sind folglich 0-Mal die Planck Masse, 1 Mal die Planck-Masse, 2 Mal die Planck-Masse usw. Ähnlich wie die Obertöne eines Geigen-Stücks auch alle Vielfache eines Grundtons (oder einer Grundfrequenz) sind. Im ganz Kleinen müsste das Sein einem riesigen Geigerorchester und das gespielte Stück unserem Universum ähneln.

# Wie hört sich ein Gluon an?
Wie klingt eine negative Ladung?
In gewissen Stringtheorien stellen Schwingungen niedrigster Energie bei offenen Strings Tachyonen dar. Andere Schwingungsmoden assoziieren dann beispielsweise Photonen oder ein Higgs-Teilchen.
- Stärke
Und genau hierin liegt die große Stärke der Stringtheorie. Die Strings sind ein radikal neuer, origineller und sehr eleganter Ansatz zur Beschreibung der Beschaffenheit von Raum, Kraft und Materie. Denn nicht nur die Materie-, auch alle Kraftteilchen folgen den Anregungen der Strings. Auch W- und Z-Teilchen sind somit nur Ausdruck der vibrierenden Strings. Demzufolge werden wirklich alle Teilchen des Standardmodells von der Stringtheorie erklärt. Entsprechend Occam's Razor ist diese vereinheitlichte Theorie aller Materie und aller Kräfte innerhalb der Stringtheorie ein großer Pluspunkt für selbige. Alles besteht aus Saiten, nur die Schwingungsfrequenz ist anders.
2. als Quantengravitation
Fast neben der Entwicklung her bemerkte man, dass die Stringtheorie auch eine Quantengravitationstheorie ist. Denn 1974 entdeckten die Physiker John Schwarz und Joël Scherk ein Schwingungsmuster, dessen simulierte Eigenschaften näherungsweise mit dem des Gravitons, dem Botenteilchen der Gravitation, kompatibel ist. Es ist ein sehr energiearmes Schwingungsmuster und da die Stärke der Gravitationskraft proportional zur Stringlänge ist, müssen die „Graviton-Strings“ äußerst kurz sein. Dies alles bedeutet, dass die Gravitationskraft im quantenmechanischen Rahmen der Stringtheorie beschrieben werden kann. Neben der Vereinheitlichung aller Kräfte und Materie ist die Identifikation eines Stringschwingungsmusters als Gravitationskraft das große Verdienst der Stringtheorie.
Kurz wollen wir darauf eingehen, wie geschickt die Stringtheorie dahingehend zwischen allgemeiner Relativitätstheorie und Quantenmechanik vermittelt. Wie bereits erläutert ist ein großer Streitpunkt, dass die ART eine glatte Raumzeit, die Quantenmechanik jedoch eine Art Quantenschaum aufgrund der Nullpunktfluktuationen in Anwendung auf das Gravitationsfeld, der turbulenter wird, umso näher man heranzoomt, einnimmt. Während nulldimensionale Teilchen in das Netz zu den wilden Gegenden unterhalb der Planck-Länge fallen können, hat die Stringtheorie dieses Problem nicht. Dafür müssen wir uns die Gravitation auf subatomarer Ebene als eine Ansammlung wild umherfliegender Gravitonen vorstellen, genauso wie man bei Wasser auf molekularer Ebene die chemischen Elemente Wasserstoff und Sauerstoff betrachtet. Nach der Stringtheorie hat ein Graviton-String eine räumliche Ausdehnung und da es die fundamentale Matrjoschka-Puppe ist, aus der sich die Gravitation zusammensetzt, macht es keinen Sinn mehr die Gravitation unter Skalen unterhalb der Planck-Länge zu untersuchen. Es ist, als ob ein Discounter für ein Produkt 19,005€ verlangen würde – theoretisch möglich, aber praktisch nutzlos. Und da die heftigen Fluktuationen nur bei Abständen kürzer der Planck-Länge problematisch werden, umgeht die Stringtheorie das Problem mit der schäumenden Raumzeit.
# die Reise in den Mikrokosmos endet bei den Strings, dies löst einige Probleme.
Im Groben waren dies die Stärken der Stringtheorie, sie weist aber auch viele Probleme, ein Stringtheoretiker würde sagen Herausforderungen für die andauernde Stringforschung, auf.
3. Superstringtheorie
Damit eine konsistente Stringtheorie formuliert werden kann, müssen zusätzliche Beziehungen zwischen den Teilchen postuliert werden. Diese werden unter dem Begriff Supersymmetrie subsumiert und finden sich auch in anderen vereinheitlichten Theorien wieder. Es zeigt sich theoretisch, dass Stringschwingungsmuster immer in Paaren vorkommen, deren Spin sich je um eine halbe Einheit unterscheidet. Für eine Schwingung mit dem Spin 0,5 existiert also eine Schwingung mit Spin 0 usw. Die Stringtheorien der supersymmetrischen Teilchen werden als Superstringtheorien bezeichnet, ihre Strings als Superstrings. Bislang sprechen jedoch alle Experimente gegen die Existenz von „SUSY“.
4. Dimensionen
Ein weiterer theoretischer Aspekt der Superstringtheorie, für den es in der Realität keine Entsprechung zu geben scheint, ist die Anzahl der benötigten Dimensionen.
- Dimension (phy.)
Die Superstringtheorie beinhaltet eine unentbehrliche Gleichung, die zunächst etwas über die Anzahl unabhängiger Schwingungsmuster im Zusammenhang mit den Raumdimensionen aussagt. Gemeinhin wird davon ausgegangen, dass das Universum drei Raum- plus eine Zeitdimension besitzt. Aber in einem Universum mit nur drei Raumdimensionen ist die Zahl der realisierbaren Schwingungsmuster zu klein für unser Universum. Erst mit neun Raumdimensionen kann die Superstringtheorie mathematisch konsistent auf unser Universum angewendet werden. Auf diese Weise bestimmt die Superstringtheorie die Anzahl der nötigen Dimensionen, damit sie für unser Universum gültig sein kann. Mitsamt der Zeit braucht es in einem Superstring-Universum also zehn Informationseinheiten, um den Aufenthaltsort eines Objektes zu definieren. Damit bringt uns die Superstringtheorie in eine komplett neue Situation. Noch nie zuvor hat eine physikalische Theorie mathematisch etwas über die Zahl der Dimensionen ausgesagt, auch keine andere Quantengravitationstheorie. Man ging bislang stillschweigend davon aus, dass das Universum drei Raumdimensionen habe. Die erste aufsehenerregende Theorie, die darüber überhaupt etwas aussagt, sagt aber gerade etwas anderes.
# Eine auf unsere Welt anwendbare Stringtheorie
braucht mindestens neun Raumdimensionen!
Doch damit nicht genug. In der theoretischen Physik ist
man sich nicht einmal ganz einig, wie viele Extradimensionen das Universum überhaupt braucht. Eine Nicht-Super-Bosonenstringtheorie beispielsweise bedarf ganze 26 Raumzeitdimensionen. Mit
unseren 3 Dimensionen, der Länge, der Breite und der Höhe, ist es, wenn es nach der Stringtheorie geht, aber sicher nicht getan.
Calabi-Yau-Raum
Die Mathematik hinter der Stringtheorie bestimmt nicht nur, wieviel Raumdimensionen unser Universum haben soll, sondern auch deren möglichen Formen. Nur in einem der sogenannten Calabi-Yau-Räume können die Stringschwingungsmuster bzw. Teilcheneigenschaften angemessen beschrieben werden. Calabi-Yau-Räume sind komplexe Mannigfaltigkeiten, die vor der Entwicklung der Stringtheorie bloße theoretische Konstrukte der Mathematik waren. Nun bekommen sie eventuell eine reale Bedeutung. Welchem Calabie-Yau-Raum die reale Bedeutung jedoch zukommen soll, ist noch nicht geklärt. Die der Stringtheorie zugrundeliegenden Gleichungen präferieren keinen der sechsdimensionalen Gebilde.
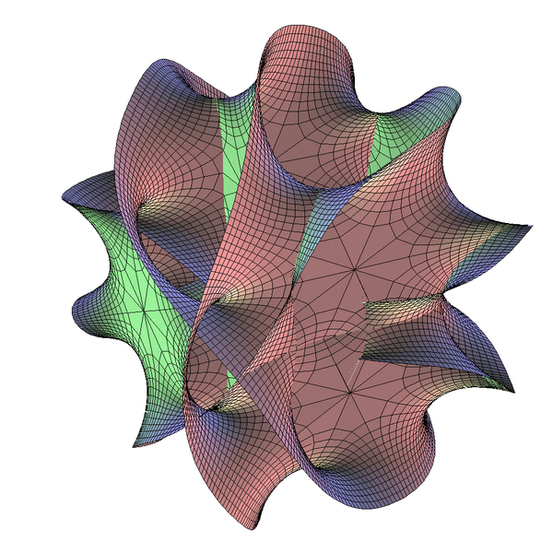
Wo stecken die zusätzlichen Dimensionen?
Eventuell haben Sie die letzten beiden Abschnitte mit einem gewissen Stirnrunzeln gelesen. Wenn Sie mit ihrem Date: „5th Avenue (Länge), dritter Stock (Höhe), fünftes Zimmer von links (Breite) um 18 Uhr (Uhrzeit)" ausmachen, ist der Treffpunkt arrangiert. Auch alle Querstraßen sind durch eine Kombination dieser Angaben beschreibbar. Unsere Erfahrung lehrt uns also, dass es nur vier Raumzeitdimensionen gibt, da wir uns in keiner anderen zu bewegen scheinen. Empirisch spricht absolut nichts für die Existenz von weiteren Extradimensionen, wo also sollen sich diese versteckt halten?

Die meisten Stringforscher gehen davon aus, dass sie Extradimensionen extrem klein bzw. „aufgewickelt“ sind und relativen Riesen deshalb nicht auffallen. Um diesen komplizierten Sachverhalt irgendwie veranschaulichen zu können, bemühen Sie die einfache Analogie des Haares. Auf dem ersten Blick scheint ein Haar eindimensional zu sein. Es erstreckt sich in die Länge, Breite und Höhe, aber sind mit dem bloßen Auge kaum zu erkennen. Erst wenn das Haar unter einem Mikroskop betrachtet wird, offenbart es seine Ausdehnungen in Breite und Höhe. Um die zusätzlichen Raumdimensionen der Superstringtheorie sehen zu können, fehlt uns derzeit das ausreichend leistungsfähige Mikroskop, was sie aber nicht inexistent macht. Oft wird dann noch angeführt, man solle sich die aufgewickelten Dimensionen mithilfe eines Seils visualisieren. Auch dieses ist aus kleineren Strängen aufgewickelt. Von weitem sieht man das nicht, aber zoomt man näher heran, so fällt auf, dass man sich von jedem Punkt auf dem Seil aus auch länglich in / gegen Richtung des Uhrzeigersinns bewegen kann. Und, dass man bei jeder anderen Form der Ortsänderung auf der Seiloberfläche auch immer ein wenig in diese Extrarichtung bewegt. Diese Extrarichtung ist nur so klein, dass es einem zunächst gar nicht auffällt, bewegt man sich auf ihr.
Genauso kann es sein, dass der Calabi-Yau-Raum an jedem Punkt im Universum heftet. Und wenn Sie einen Schritt gehen, so bewegen Sie sich auch durch die restlichen sechs Raumdimensionen. Da wir den Calabi-Yau-Raum dabei aber so schnell und so viele Male durchschreiten, bleibt uns unsere Bewegung in den Extradimensionen unbemerkt.
Wie es sich zu Zeiten des Urknalls mit den Dimensionen verhielt, ist uns empirisch unzugänglich. Wir können die Entwicklung des Universums aber mathematisch zurückrechnen und so etwas über die frühe Beschaffenheit von Raum und Dimensionen erfahren. Eine Konsequenz aus der unendlichen Dichte zur Geburtsstunde des Universums ist, dass auch die heute großen Dimensionen damals bedeutend komprimiert waren. Wahrscheinlich gar es unmittelbar nach dem Urknall keinen Unterschied zwischen den üblich-vertrauten und den Extradimensionen. Erst mit der daraufhin folgenden Expansion bzw. kosmologischen Evolution müsste sich ein Unterschied zwischen den beiden Dimensionstypen herauskristallisiert haben. Warum ist nicht geklärt. Die zahlreichen, dargelegten ad-hoc-Hypothesen zur Anzahl und Form der Dimensionen scheinen eine Schwachstelle der Stringtheorie zu sein. Aber vielleicht verhelfen gerade sie ihr auch zu ihrem finalen Erfolg. Unter interessierten Laien ist es bekannt, dass am LHC Zustände des Urknalls simuliert werden. Vielleicht können wir also mit deren Hilfe empirisch das Geheimnis der Extradimensionen lüften. Wenn nun die Existenz einer fünften, sechsten oder noch mehrerer Dimension bei hochenergetischen Prozessen in einem Teilchenbeschleuniger nachgewiesen wird, ist ein Postulat der Stringtheorie empirisch falsifiziert worden. In diesem Fall würde die Stringtheorie schlagartig mehr Beachtung geschenkt bekommen.
Das Bemühen solcher Experimente heißt nicht zwangsläufig, die Extradimensionen seien klein. Auch dies ist nur eine praktische Vermutung, weil wir denken sie nicht wahrnehmen zu können. Theoretisch ist das letzte Wort über die Größe der Extradimensionen noch nicht gesprochen. Sie könnten auf geladenen Membranen in höherdimensionalen Kontinua liegen. Als Hobbyphilosoph möchte ich noch in die Diskussion einbringen, dass möglicherweise unsere Sinne für die Extradimensionen nicht empfindlich sein könnten. Andere Lebewesen auf fernen Planeten wählen dann bei jeder zwischen neun Dimensionen und halten dies für das trivialste auf der Welt. Diese Annahme ist natürlich rein spekulativ.
5. M-Theorie
keine vollendete Theorie
Dem Leser ist wohl nicht entgangen, dass viele große Lücken im theoretischen Konstrukt der Stringtheorie klaffen und sie weit davon entfernt ist eine vollendete Theorie darzustellen. Viele Stringforscher haben daher das Gefühl den Grundbaustein der Stringtheorie noch nicht entdeckt zu haben. Bei der speziellen Relativitätstheorie ist es die Lichtkonstante, bei der allgemeinen das Äquivalenzprinzip von Gravitation und Beschleunigung und bei der Quantenmechanik die Heisenbergsche Unschärferelation. Dieses charakterisierende, alle anderen logisch verknüpfende Element scheint bei der Stringtheorie aber zu fehlen. „Noch zu fehlen“, würde der Stringforscher an dieser Stelle einwenden, denn er und seine Kollegen laufen keineswegs auf der Stelle, sondern denken die Stringtheorie mit dem fortschreitenden Verständnis der ihr zugrunde liegenden Mathematik immer besser zu verstehen.
die 5 Stringtheorien
Desweiteren ist es dem aufmerksamen Leser vielleicht aufgefallen, dass öfters von Stringtheorien die Rede war. Dies ist ein weiterer Knackpunkt des Forschungsgebietes. Bisher sind wir so vorgegangen, als gäbe es eine einzige, aber es gibt fünf verschieden Varianten der Stringtheorie: Typ I, Typ IIA, Typ IIB, E-heterotisch und O-heterotisch. Was bisher beschrieben wurde, trifft auf jede dieser Typen zu, jedoch bestehen die übrigen Unterschiede keineswegs in Nuancen. Das große Problem ist, dass es zur adäquaten Beschreibung des einen Phänomens die eine, zur Klärung eines anderen Phänomens aber eine andere Variante braucht. Der Anspruch, dem sie als vereinheitlichte Theorie jedoch genügen sollte, ist die einheitliche Beschreibung des Universums durch eine und nur eine Theorie. Und dies ist ein grundsätzliches Problem der Theorie mit den Strings. Denn auch wenn eines fernen Tages tatsächlich eine der fünf Stringtheorien empirisch als die richtige verifiziert werden sollte, so bleibt die Frage, ob den anderen Versionen, die theoretisch ebenso möglich wären, nicht auch irgendeine Bedeutung zuzumessen sei. Vielleicht finden sie in Paralleluniversen ihre Geltung? Und gibt es noch andere, unentdeckte Variationen der Stringtheorie?
die M-Theorie
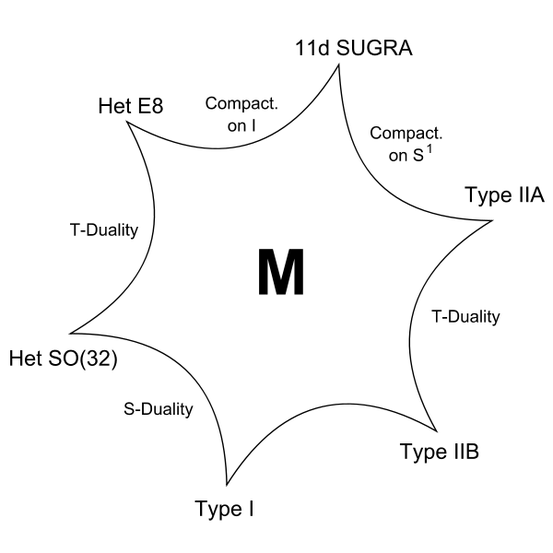
Es leuchtet aber ein Silberstreifen am Horizont. 1995 referierte der Stringpionier Edward Witten an der University of Southern Californa. Er sprach neue revolutionäre neue Ideen bezüglich der Zusammenhänge zwischen den fünf Superstringtheorien an. Wie Witten nachwies, widersprechen sich die fünf Stringtheorien nämlich überhaupt nicht, sondern sind ausschließlich verschiedene Möglichkeiten der mathematischen Formulierung einer im wahrsten Sinne des Wortes einzigartigen Theorie. Damit leitete Witten die zweite Superstringrevolution ein.

Man kann die fünf Superstringtheorien mit den Übersetzungen einer Urschrift in fünf verschiedene Sprachen vergleichen. Diese Kollation veranschaulicht Zweierlei. Erstens hielt man die fünf Stringtheorien zunächst nur für gegensätzlich, da es uns an Sprachkenntnissen fehlte. Mit Witten haben aber wir begonnen, ein String-Wörterbuch zu schreiben. Zweitens sind alle Theorien ihrem Anspruch gemäß unvollständig, da jede Übersetzung fehlerbehaftet ist. Die eine Überlieferung in eine andere Sprache übersetzt vielleicht den einen Absatz gut, hat aber prinzipiell keine hinreichenden Worte, um die Wortspiele des zweiten sinngemäß wiederzugeben. Manchmal leistet dies eine andere Übersetzung, ab und zu aber auch gar keine und man braucht das Original. Wie in sprachlichen Übersetzungen, so kommt auch keine der mathematischen Übersetzungen an den Quelltext ran.

Die Originaltheorie, aus der sich alle herkömmlichen fünf Stringtheorie ableiten lassen, nennt sich bis auf weiteres die M-Theorie. Es muss jedoch eingestanden werden, dass die Kenntnis der gegenwärtigen Physik gegenüber der M-Theorie nochmals nebulöser ist, als es sie über die herkömmlichen Stringtheorien sowieso schon war. Aus diversen Gründen geht man jedoch davon aus, dass eine widerspruchsfreie M-Theorie existiert und sich der Nebel um sie durch menschlich-geistige Kraftaufwendungen sukzessiv lösen lässt. Die M-Theorie ist somit vorerst einmal der Versuch einer theoretisch-synthetischen Verallgemeinerung und Erweiterung der Stringtheorien. Sie ist ausdrücklich keine neue, im Sinne einer eigenständigen Theorie! Aber nur sie kann alles originalgetreu beschreiben. Und da wir sie zu Teilen kennen, können wir mit ihr mehr erklären als noch zuvor mit den approximativen Stringtheorien.
# Wofür das „M“ in M-Theorie steht ist nicht eindeutig festgelegt.
Vielleicht Master? Membran? Mega? Mystery? Matrix?
Ein letztes Mal noch möchte ich Sie mit Dimensionen, Lösungen und möglichen Paralleluniversen belästigen. Zunächst die Dimensionen. Aus Umständen, die uns hier nicht weiter interessieren sollen, generiert die M-Theorie noch eine zusätzliche Raumdimension. Neun plus eine Raumdimension, plus eine Zeitdimension macht insgesamt elf Raumzeitdimension. So, kurz und schmerzlos. Ich nehme jedoch an, dass sich abgesehen seiner mathematisch-strukturellen Bedeutung das Bild vor ihrem inneren Auge von einem zehn- zu einem elfdimensionalen Universum nicht groß geändert hat.
Nun zu den möglichen Lösungen und Paralleluniversen. Die Stringtheorie besitzt ungeheuer viele Lösungen, vielleicht 2^500, was unvorstellbar viel mehr ist als die Anzahl der Atome im Universum! Da auch
bisher die M-Theorie keine wirklich empirisch falsifizierbaren Postulate mit sich bringt, wissen wir nicht, ob und wenn ja, welche dieser Lösungen unser Universum beschreibt. Viele Physiker
versuchen sich mit der Annahme, jede Lösung beschreibt eins von unzählbar vielen Paralleluniversen, zu retten. (Die
M-Theorie will auch eine sogenannte Theory of Everything sein, deren zentrales Anliegen es ist zu erklären, dass sich die Werte der Naturkonstanten
sehr wahrscheinlich oder vielleicht sogar automatisch, aber nicht willkürlich als die richtigen ergeben (Siehe auch:
anthropisches Prinzip).) Mit so vielen Paralleluniversen sollte schlussendlich statistisch ein Universum
darunter sein, das unsere Naturkonstanten aufweist. So das Argument. Das ist aber starke Metaphysik, keine
Physik. Ehrlicher von diesen Physikern wäre es zu sagen, warum die
Naturkonstanten gerade die Werte haben, die sie haben, können wir gegenwärtig nicht klären. Wir geben aber unser Bestes, um irgendwann darauf eine Antwort zu finden.
6. Fazit
Das Schicksal der Stringtheorie hängt meiner Ansicht nach gegenwärtig noch in der Waage. Auf der einen Seite steht ihr enormes Potential Materie- und Kraftteilchen, Quantenmechanik und Gravitation zu vereinheitlichen und noch vieles mehr. Auf der anderen Seite ihre praktische Unzugänglichkeit und theoretische Unvollständigkeit uvm. (wenn man so will Unzulänglichkeiten). Metaphorisch gesprochen könnte es ein Zünglein an der Schicksalswaage sein, die selbige für oder gegen die Gunst der Stringtheorie kippen lässt. Dieses Zünglein könnte die plötzliche Entdeckung einer empirischen Falsifikationsmöglichkeit sein, woraufhin sich Strings und Membranen als nicht real nachweisen lassen und die Stringtheorie somit als unheimlich komplizierter, mathematischer Irrweg enttarnt ist. Oder es der Grundbaustein der Stringtheorie, die selbige im Lichte der M-Theorie alle bisherigen Probleme in Luft auflöst.
In Anbetracht der Fragen, vor der die Stringforschung noch zu stehen scheint, ist das, was wir bereits meinen zu wissen, herzlich wenig. Doch zumindest dieses Quantum wollte ich dem geneigten Leser, dem an dieser Stelle ein Lob ausgesprochen ist, dafür, dass er es bis hierhin geschafft hat, etwas näher bringen. Mein Anspruch war es dabei, dass auch Menschen, die physikalisch tiefgrün hinter den Ohren sind etwas aus der Lektüre dieses Textes mitnehmen können. Ich hoffe, das ist mir ein wenig gelungen. Dem physikalisch bereits etwas geschulteren Leser sei noch um Verzeihung gebeten. Zur kleinen Rechtfertigung sei angemerkt, dass wenn man etwas einfacher und anschaulicher erklären möchte, so ist es dabei unausweichlich, dass Information verloren geht. Wäre dem nicht so, dann wäre die professionelle theoretische Physik neben der Populärwissenschaft überflüssig. Eine große Herausforderung bei einem solchen Unterfangen, die Stringtheorie Menschen, die Arbeit und Familie und damit keine Zeit haben sich in die eigentlichen mathematischen Sachverhalte einzulesen, näher zu bringen, ist sicherlich das zu Beschreibende von einer mathematisch-abstrakten auf eine anschaulichere Ebene zu bringen. Dies wiederum liegt darin begründet, dass die Stringtheorie ausschließlich Entitäten fernab unserer Alltagsvorstellung postuliert.
Hier noch etwas für alle.
7. Verweise
- Quantengravitation: Der „Erklärungspfeil“ bisheriger Vereinheitlichungen scheint auf eine tatsächlich existente Quantengravitation hinauszulaufen. Die Stringtheorie ist ein vielbeachteter Ansatz zur theoretischen Beschreibung einer solchen.
- #Stringtheorien #Branen: Die M-Theorie beschreibt neben den Strings noch eine, noch eine verrücktere ontologische Grundsubstanz. In diesem Aufsatz wurde auf die Charakterisierung dieser Branen wegen dem Fokus dieser Aufsatzreihe auf Vereinheitlichungen und auch der Übersichtlichkeit halber verzichtet. Im verlinkten Artikel erfahren Sie, was Branen sind und was Branen machen.
8. Quellen
Matryoshka-Puppen: http://de.wikipedia.org/wiki/Datei:First_matryoshka_museum_doll_open.jpg
Orchester: http://de.wikipedia.org/wiki/Datei:Rotterdams_Philharmonisch_Orkest-2011.jpg
Calabi-Yau: http://de.wikipedia.org/wiki/Datei:Quintic_1.png
Papyrus: http://commons.wikimedia.org/wiki/File:Papyrus.jpg
M-Theorie: http://de.wikipedia.org/w/index.php?title=Datei:M-Theory.svg&filetimestamp=20110920171649&
Stand: 2014
 Philoclopedia
Philoclopedia

Gebhard Greiter, greiterweb.de (Samstag, 23 November 2024 09:49)
Tatsache ist, dass viele – aber keineswegs alle – Stringtheoretiker Susskinds Meinung nachvollziehbar finden. Richtig ist auf jeden Fall, dass es bisher niemand gelang, eine überzeugende de-Sitter-Lösung aus der Stringtheorie abzuleiten.
Noch ein Gesichtspunkt aber:
Genau genommen kann man aber auch gar nicht nicht mit absoluter Sicherheit ausschließen, dass unser Weltraum nicht vielleicht doch AdS (= anti-deSitter) ist: Beobachtetes, lokales Krümmungsverhalten muss ja nicht unbedingt auch weiträumig gegebenes sein. Mit anderen Worten: Wir werden nie mit absoluter Sicherheit ausschließen können, dass der Weltraum nicht doch hyperbolische Geometrie hat, also – weiträumig gesehen – ewig expandieren könnte.
Gebhard Greiter, greiterweb.de (Freitag, 22 November 2024 15:03)
Interessant ist, dass Leonard Susskind – er gilt schon seit 1969 als einer der Pioniere der Stringtheorie – heute nicht mehr glaubt, dass Stringtheorie unsere Welt korrekt beschreiben kann: Wir leben in einem de-Sitter-Raum, er aber sei zunehmend davon überzeugt, dass sämtliche durch Stringtheorie beschreibbaren Räume anti-de-Sitter sind. Note: Wirklich bewiesen scheint Letzteres bisher aber (soweit ich weiß) nicht zu sein.
Man höre ihn selbst in diesem Video: https://www.youtube.com/watch?v=2p_Hlm6aCok (die Werbung zu Beginn kann man überspringen).
tsSLAueP (Mittwoch, 15 November 2023 19:05)
1
tsSLAueP (Mittwoch, 15 November 2023 17:56)
1
tsSLAueP (Mittwoch, 15 November 2023 17:04)
1
tsSLAueP (Mittwoch, 15 November 2023 17:03)
1
tsSLAueP (Mittwoch, 15 November 2023 17:03)
1
tsSLAueP (Mittwoch, 15 November 2023 17:02)
1
tsSLAueP (Mittwoch, 15 November 2023 17:01)
1
tsSLAueP (Mittwoch, 15 November 2023 17:01)
1
tsSLAueP (Mittwoch, 15 November 2023 17:00)
1
tsSLAueP (Mittwoch, 15 November 2023 17:00)
1
tsSLAueP (Mittwoch, 15 November 2023 16:59)
1
tsSLAueP (Mittwoch, 15 November 2023 16:58)
1
tsSLAueP (Mittwoch, 15 November 2023 16:58)
1
tsSLAueP (Mittwoch, 15 November 2023 16:57)
1
tsSLAueP (Mittwoch, 15 November 2023 16:57)
1
abGmb7z1' OR 415=(SELECT 415 FROM PG_SLEEP(15))-- (Mittwoch, 15 November 2023 16:56)
1
0"XOR(if(now()=sysdate(),sleep(15),0))XOR"Z (Mittwoch, 15 November 2023 16:56)
1
tsSLAueP (Mittwoch, 15 November 2023 16:55)
1
tsSLAueP (Mittwoch, 15 November 2023 16:53)
1
tsSLAueP (Mittwoch, 15 November 2023 16:52)
1
tsSLAueP (Mittwoch, 15 November 2023 16:52)
1
tsSLAueP (Mittwoch, 15 November 2023 16:51)
1
tsSLAueP (Mittwoch, 15 November 2023 16:51)
1
tsSLAueP (Mittwoch, 15 November 2023 16:50)
1
tsSLAueP (Mittwoch, 15 November 2023 16:49)
1
tsSLAueP (Mittwoch, 15 November 2023 16:49)
1
tsSLAueP (Mittwoch, 15 November 2023 16:48)
1
tsSLAueP (Mittwoch, 15 November 2023 16:48)
nQWBfQk3') OR 367=(SELECT 367 FROM PG_SLEEP(15))--
tsSLAueP (Mittwoch, 15 November 2023 16:47)
-5 OR 53=(SELECT 53 FROM PG_SLEEP(15))--
tsSLAueP (Mittwoch, 15 November 2023 16:47)
-1); waitfor delay '0:0:15' --
tsSLAueP (Mittwoch, 15 November 2023 16:46)
0"XOR(if(now()=sysdate(),sleep(15),0))XOR"Z
tsSLAueP (Mittwoch, 15 November 2023 16:46)
0k6rbe5P
tsSLAueP (Mittwoch, 15 November 2023 16:45)
1
tsSLAueP (Mittwoch, 15 November 2023 16:45)
1
tsSLAueP (Mittwoch, 15 November 2023 16:44)
1
tsSLAueP (Mittwoch, 15 November 2023 16:43)
1
tsSLAueP (Mittwoch, 15 November 2023 16:43)
1
tsSLAueP (Mittwoch, 15 November 2023 16:42)
1
tsSLAueP (Mittwoch, 15 November 2023 16:42)
1
tsSLAueP (Mittwoch, 15 November 2023 16:41)
1
tsSLAueP (Mittwoch, 15 November 2023 16:02)
1
Nanni Rasul (Samstag, 07 April 2018 12:52)
Toller Text für einen Grünschnabel wie mich!
Was ich immer noch nicht verstanden habe: warum werden die anderen Dimensionen superklein aufgerollt?
Für die Flachländer ist unsere 3. Dimension ja auch nicht aufgerollt, nur einfach nicht wahrnehmbar. Warum ist diese Vorstellung der anderen Dimensionen notwendig?
LG, Nanni ( nabafee@live.de )