Der Zahlenbereich der komplexen Zahlen ist die exakte Obermenge aller reellen und imaginären Zahlen. (Wobei die imaginären Zahlen genau genommen gar keine eigenständige Zahlenmenge bilden.)

Alle reellen Zahlen liegen auf der Zahlengeraden bzw. die Summe aller Punkte auf der Zahlengeraden entspricht alle reellen Zahlen. Reelle Zahlen sind beispielsweise 2, -4, √8, π (Pi) usw.

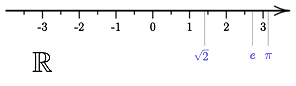
In einigen Fällen kommt man mit reellen Zahlen jedoch nicht weiter. Etwa bei der Gleichung x² = - 1. Keine reelle Zahl ist eine Lösung für x. Weil egal ob man eine beliebige positive oder eine beliebige negative Zahl R mit sich selbst multipliziert, das Ergebnis ist immer ≥ 0, also ≠ – 1. „Plus mal Plus gibt Plus und Minus mal Minus gibt Plus“ - lernt man schon in der Schule.

Das x² = -1 steht aber noch im Raum und es ist durchaus legitim nach der Zahl zu fragen, deren Quadrat minus eins ergibt. Dass die reellen Zahlen keine Antwort auf diese Frage wissen beweist zunächst nur, dass nicht jede quadratische Gleichung eine reelle Lösung hat. Lange Zeit über waren reelle Zahlen aber die einzig bekannten Zahlen. Wie gezeigt braucht es aber einer Erweiterung des Zahlenbereiches, z.B.: um gewisse quadratische Gleichungen lösen zu können. Also hat man sich einfach eine neue Zahl eingeführt und so definiert:

i = √-1

i ist eine imaginäre Einheit. Imaginäre "Zahlen" sind komplexe Zahlen, die quadriert eine nicht-positive reelle Zahl ergeben. Sie sind nicht nur einer der wichtigsten Konzepte in der modernen Mathematik, sondern beispielsweise auch in der Quantenmechanik oder Elektrotechnik von großer Bedeutung.

Zusammen mit den reellen bilden die imaginären Zahlen die Menge der komplexen Zahlen. Andersherum ausgedrückt: Die komplexen Zahlen erweitern den Zahlenbereich der reellen Zahlen um die Summe aller imaginären Zahlen.

Jede komplexe Zahl C kann folglich dargestellt werden als: C = a + bi. Dabei ist a der Realteil und b der Imaginärteil der komplexen Zahl C. A und b sind immer reele Zahlen, der Multiplikator von b i eine imaginäre Einheit.

Setzt man für b 0 ein, bekommt man für c natürlich eine reelle Zahl heraus. Also ist die Menge der reellen Zahlen R eine Teilmenge der komplexen Zahlen C.

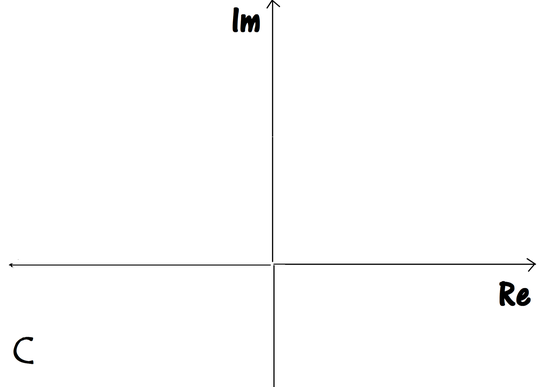
Um komplexe Zahlen geometrisch zu visualisieren, zu interpretieren und mit ihnen operieren zu können, verwendet man eine komplexe Ebene – die Gaußsche Zahlenebene.

Erinnern wir uns an die Formel: C = a + bi. Die „x-Achse“ der GZ entspricht dem Realteil a und heißt hier reelle Achse und die „y-Achse“ beinhaltet die imaginäre Einheit i und heißt imaginäre Achse.

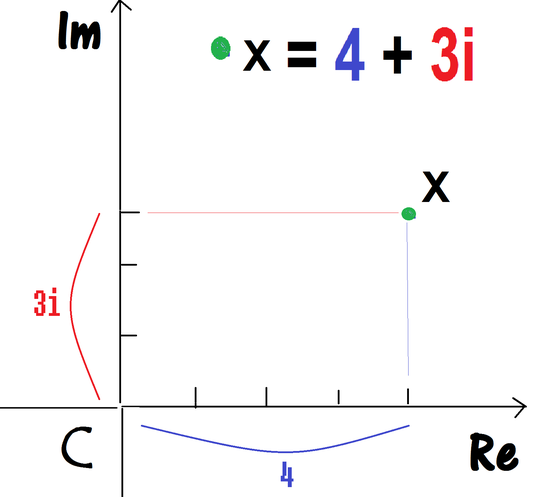
Alle reellen Zahlen lassen sich als Punkte auf der Zahlengerade Re finden. Diese haben wir nun durch die Dimension Im bzw. die imaginären Zahlen erweitert. Die komplexen Zahlen finden sich in der kompletten Gaußschen Zahlenebene. Meist werden sie dort als Punkte oder Vektoren dargestellt.

• Rechnen mit komplexen Zahlen

• Ontologie: Obwohl die komplexen Zahlen in vielen Forschungs- und Entwicklungsfeldern erfolgreiche Verwendung finden, ist uns ihre reale Entsprechung noch nicht ganz klar.

• Tadryon, Luxon, Tachyon: Hypothetischen Teilchen werden aber bereits komplexe Zahlen zugeschrieben. Die quadrierte Masse eines Tachyons beispielsweise müsste negativ sein.

• Raum & Zeit: Auch die sog. imaginäre Zeit kann nur mit Hilfe von imaginären Zahlen gemessen werden.

• Universum: Nach der Idee der keine-Rand-Bedingung ist das Universum von endlicher Ausdehnung, besitzt in der imaginären Zeit aber keinen Rand.

• Universalienfrage der Mathematik: Gibt es (komplexe) Zahlen?

• Leibniz: Gottfried Wilhelm Leibniz sah in den komplexen Zahlen ein „Amphibium zwischen Sein und Nichtsein.“

Gliederung