Das Induktionsproblem (auch: Humesches Problem, Hume-Problem) ist ein erkenntnistheoretisches Grundproblem, das in der Frage besteht, ob und wann logisch induktive Schlüsse verlässlich bzw. rational sein können. 

Es wurde im 18. Jahrhundert vom Philosophen David Hume in A Treatise of Human Nature formuliert. Auch wenn Hume sich dem Empirismus verschrieben sah und das Problem in diesem formulierte, betrifft es alle Philosophien und Wissenschaften, die Induktionsschlüsse als gültige Beweisverfahren anerkennen.

Ein Induktionsschluss kann dabei formal so dargestellt werden:

P1. r% aller n bisher beobachteten Fs waren Gs.

K1. r% aller Fs sind (ungefähr; wahrscheinlich) Gs.

Ein typisches Beispiel für einen Induktionsschluss:

P1. 100% aller n bisher beobachteten Schafe (S1, S2, S3, ...Sn) waren weiß.
K1. Also: 100% aller Schafe sind (ungefähr; wahrscheinlich) weiß.

Dieser Schluss ist offenbar nicht-zwingend. Denn auch eine noch so hohe Anzahl n an bisher beobachteten weißen Schafen macht es nicht zwingend, dass alle Schafe weiß sind. In der Tat könnte bereits das n+1.te Schaf schwarz sein!

Aber dieser Schluss lässt sich zwingend machen, indem man das Prinzip der Gleichförmigkeit der Natur (kurz: PUA) annimmt. Dieses Prinzip besagt, dass Unbeobachtetes und Zukünftiges dem Beobachteten und Vergangenem (weitgehend) ähnlich sein werden. Auf unser Beispiel gemünzt besagt PUA, dass überhaupt alle Schafe, wie auch die bisher beobachteten, (weiß) sein werden:

P1. 100% aller n bisher beobachteten Schafe (S1, S2, S3, ...Sn) waren weiß.

P2. Alle Schafe sind den bisher beobachteten Schafe (weitgehend) ähnlich.
K1. Also: 100% aller Schafe sind (ungefähr; wahrscheinlich) weiß.

David Hume hat aber auf das Problem hingewiesen, dass sich das PUA nicht vernünftig begründen lässt. Denn es lässt sich weder direkt a priori oder a posteriori, noch indirekt durch deduktive oder induktive Argumente rechtfertigen.

Dieses Problem der Begründung von PUA ist der Kern des Induktionsproblems.

„Es ist [..] unmöglich, dass irgendein Erfahrungsbeweis die Ähnlichkeit der Vergangenheit mit der Zukunft erweisen könnte. Mag der Gang der Dinge bislang auch noch so regelmäßig gewesen sein, so kann das allein nicht beweisen, dass es auch in Zukunft so bleiben werde."

- David Hume[1]

Ein logischer Schluss zeichnet sich allgemein dadurch aus, dass die Wahrheit der Konklusion K auf irgendeiner Weise aus der Wahrheit der Prämissen P folgt.

Dabei gibt es prinzipiell zwei Arten von logischen Schlüssen:

Bei einer Deduktion folgt die Wahrheit von K zwingend aus der Wahrheit von P.

Beispiel 1:

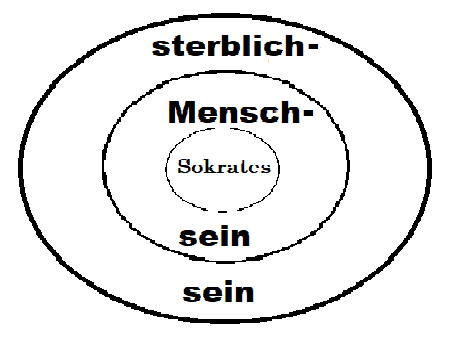
P1. Alle Menschen sind sterblich.
P2. Sokrates ist ein Mensch.
K1. Sokrates ist sterblich.

Wenn es also wahr ist, dass alle Menschen sterblich sind und dass Sokrates ein Mensch ist, dann ist es auch mit Notwendigkeit wahr, dass Sokrates sterblich ist.

1. Deduktive Schlüsse sind in diesem Sinne also wahrheitskonservierend.

Denn ihre K´s gehen nicht über das hinaus, was in ihren P´s schon impliziert ist.

Wenn also alle Menschen sterblich sind und Sokrates ein Mensch ist, dann steckt in den Prämissen bereits implizit drinnen, dass Sokrates sterblich ist.

2. Deduktive Schlüsse sind in diesem Sinne aber nicht-gehaltserweiternd.

Bei einer Induktion folgt die Konklusion K nicht-zwingend aus der Prämisse P.

Beispiel 2:

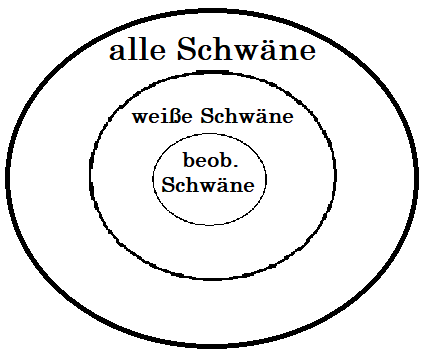
P1. Alle bisher beobachteten Schafe (S1, S2, S3, …, Sn) waren weiß.
K1. Für alle Schafe gilt: Schafe sind weiß.

Wenn es also wahr ist, dass alle bisher beobachteten Schafe Sn weiß waren, dann ist es nicht mit Notwendigkeit wahr, dass überhaupt alle Schafe Sx weiß sind. 

1. Induktive Schlüsse sind in diesem Sinne nicht-wahrheitskonservierend.

Denn ihre K gehen über das hinaus, was in ihren Prämissen impliziert ist.

Wenn also alle bisher beobachteten Schafe Sn weiß waren, dann steckt in dieser Prämisse nicht bereits implizit drinnen, dass überhaupt alle Schafe weiß sind.

2. Induktive Schlüsse sind in diesem Sinne aber gehaltserweiternd.

Also: Induktionen sind nicht-wahrheitskonservierend, aber gehaltserweiternd.

Denn ihre Prämissen "erzwingen" oder "implizieren" nicht die Konklusion.

Dieses Doppelcharakterisierung trifft auf mehrere induktive Schlussarten zu:

1. enumerativ: Alle beobachteten F sind G. Also sind alle F G.

2. statistisch: x% aller beobachteten F sind G. Also sind X% aller F G.

3. projektiv: Alle bisher beobachteten Fn waren G. Also wird auch Fn+1 G sein.

Die Abduktion kann als vierter Typus induktiver Schlüsse aufgefasst werden.[2]

Beispiel 3:

P1. Der Käse ist weg, obwohl ich ihn noch nicht gegessen habe.
P2. Wenn eine Maus auf dem Tisch war, ist der Käse weg.
K1. Ergo: Eine Maus war auf dem Tisch.

4. abduktiv: G ist die beste Erklärung für F. Also ist G wohl die Erklärung für F.

Problem: Die beste Erklärung ist nicht unbedingt die zutreffende. Der Käse könnte auch deshalb weg sein, weil mein Kind oder Aliens ihn gegessen haben.

Also: Abduktionen sind nicht-demonstrativ, aber gehaltserweiternd.

Zwischenfazit: Wir Menschen sind also prinzipiell nicht dazu in der Lage, sichere Schlüsse zu ziehen, die uns darüberhinaus noch was Neues über die Welt sagen!

Bei einem Fehlschluss folgt die Konklusion gar nicht aus den Prämissen.

Beispiel 4:

P1. Wenn etwas eine Katze ist, dann ist es auch ein Säugetier.

P2. Flipper ist ein Säugetier.

K1. Flipper ist eine Katze.

Problem: Fehlschlüsse sind nicht-demonstrativ, da die Wahrheit ihrer Prämissen die ihrer Konklusionen nicht garantieren kann. Und Fehlschlüsse sind gehalts-erweiternd, da der Gehalt ihrer Konklusionen den ihrer Prämissen übersteigt.

Frage: Wie lassen sich akzeptable induktive und ebenfalls nicht-demonstrative, gehaltserweiternde Schlüsse wie in den Beispielen 2 und 3 von offenkundigen Fehlschlüssen wie in Beispiel 4 abgrenzen?

In seinem 1748 erschienen Werk "Eine Untersuchung über den menschlichen Verstand" bemerkte David Hume als Erster, dass ein solcher Abgrenzungsversuch fundamentale philosophische Probleme nach sich zieht. Viele dieser Probleme sind nach wie vor ungelöst[3], insbesondere das sogenannte Induktionsproblem bereitet vielen Logikern und Wissenschaftstheoretikern immer noch großes Kopfzerbrechen. Später kamen noch Hempels- und Goodmans-Problem hinzu.

Das Induktionsproblem kann als die obige Frage aufgefasst werden, ob sich induktive Schlüsse überhaupt von glatten Fehlschlüssen abgrenzen lassen.

Die finale Antwort der Philosophie auf dieses Frage steht noch aus. Charlie D. Broad spricht deshalb auch davon, dass die Induktion der Siegeszug der Naturwissenschaften und gleichzeitig der Skandal der Philosophie ist.[4]

Beispiel: Die Gravitationskraft wird anhand zuverlässiger Methoden gemessen. Dabei kommt jedes Mal ein Wert um 6,674 * 10^-11 m³ / (kg*s²) heraus.

Daraus schlussfolgert der theoretische Physiker nun ein allgemeines Naturgesetz:

P1. An allen bisherigen Tagen T1, T2, T3, ... Tn betrug die Gravitationskonstante in etwa 6,674 * 10^-11 m³ / (kg*s²).

K1. Generell gilt: Die Gravitationskonstante beträgt in etwa 6,674*10^-11.

Dieser Induktionsschluss ist offensichtlicherweise nicht-demonstrativ.[5]

Er kann aber offenbar durch eine Zusatzprämisse P2 gültig gemacht werden:

P1. An allen bisherigen Tagen T1, T2, T3, ... Tn betrug die Gravitationskonstante in etwa 6,674*10^-11 m³ / (kg*s²).

P2. Die Gravitationskonstante ist raumzeitlich nicht-variabel.

K1. Generell gilt: Die Gravitationskonstante beträgt in etwa 6,674*10^-11.

Also: Ob dieser Schluss gültig ist, hängt von der Wahrheit von P2 ab. P2 ist aber wieder eine Form des Prinzips der Gleichförmigkeit der Natur. Ob induktive Schlüsse gültig sind, hängt also vom Prinzip der Gleichförmigkeit der Natur ab.

Hume selbst entwarf folgendes Beispiel für einen nicht-demonstrativen Schluss:

P1. In der Vergangenheit hat mich Brot stets genährt.
K1. Ergo: Brot wird mich auch in Zukunft immer nähren.

Die Grundstruktur dieses Schlusses ist diese hier:

P1. In der Vergangenheit hat die Erfahrung stets gelehrt, dass x.

K1. Ergo: x wird auch in Zukunft der Fall sein.

Humes Punkt ist nun, dass dieses Argument – ganz ähnlich wie im Beispiel mit der Gravitationskonstante – auf einer entscheidenden Zusatzprämisse P2 beruht: 

P1. In der Vergangenheit hat die Erfahrung gelehrt, dass x.

P2. Die Zukunft wird so sein wie die Vergangenheit.

K1. Ergo: x wird auch in Zukunft der Fall sein.

Die Leistung von Hume ist also, als Erster auf den Umstand hingewiesen zu haben, dass "alle unsere Erfahrungsschlüsse von der Voraussetzung ausgehen, dass die Zukunft mit der Vergangenheit gleichförmig sein werde."[6]

Anders formuliert: Alle nicht-demonstrativen Schlüsse beruhen auf der Voraussetzung des Prinzips der Uniformität der Natur (kurz: PUA).

Denn: Wenn sich die Natur nicht zumindest annähernd gleichförmig verhält, ist es sinnlos, auf der Basis vergangener Erfahrungen auf die Zukunft zu schließen.

Dann machen wissenschaftliche Prognosen und Projekte genauso wenig Sinn wie Arbeitszeiten, Treuegeläubde oder private Verabredungen! 

„Daher ist es unmöglich, daß irgendwelche Begründungen durch Erfahrung (arguments from experience) diese Ähnlichkeit der Vergangenheit mit der Zukunft belegen können, denn all diese Begründungen beruhen ja auf der Voraussetzung (supposition) dieser Ähnlichkeit.“
- David Hume[7]

Der Induktionsschluss kann also prinzipiell auf zwei Wegen gerechtfertigt und das Induktionsproblem damit auch auf zwei Wegen gelöst werden:

Direkte Lösung: Der Induktionsschluss wird rational gerechtfertigt.
Indirekte Lösung: Das PUA wird rational gerechtfertigt.

Ich werde im Folgenden dafür argumentieren, dass beide Wege bisher nicht ziel-führend waren und das Induktionsproblem damit nach wie vor ungelöst ist!

Die deduktiven Lösungsstrategien sind bestrebt, das Induktionsproblem mit Hilfe der Deduktion zu lösen. Hierzu zählen vor allem zwei Lösungsstrategien:

1.    Die Induktion oder das PUA werden deduktiv begründet und das Induktionsproblem somit behoben.

2.    Die Induktion wird durch Deduktion substituiert und das Induktionsproblem somit trivialisiert.

Die erste Lösungsstrategie ist nicht zielführend. Denn wenn sich das PUA deduktiv begründen ließe, dann müsste es sich beim PUA um eine notwendige Wahrheit handeln. D.h. seine Negation müsste in einen Widerspruch führen.

Aber die Verneinung von PUA: "Die Zukunft wird so sein wie die Vergangenheit" enthält keinen Widerspruch. Mehr noch: Sie ist oftmals sogar empirisch wahr!

Die Negation von "Alle Bäume werden wie bisher in den Sommermonaten auch zukünftig in den Wintermonaten blühen"[8] ist bspw. empirisch wahr. Die Welt ist in einem vielfachen Wandel begriffen und Lösungsstrategie 1 nicht zielführend.

Die zweite Lösungsstrategie ist sehr umstritten. Sie besagt, dass unsere alltägliche und wissenschaftliche Erkenntnis gar nicht auf Induktion beruht. Das Induktionsproblem ist damit zwar nicht gelöst, aber auch nicht weiter von praktischem Belang. Ein wesentlicher Verfechter war Karl Raimund Popper.

Laut Popper erkennen wir die Welt (am besten), indem wir:

1.    Eine Hypothese H gewinnen - wie, ist für ihn erstmal sekundär.

2.    Aus H deduktiv eine empirische Konsequenz K ableiten.

3.    Die Konsequenz K empirisch testen.

3.1. Wenn K einer Beobachtung widerspricht, ist H falsifiziert.

3.2. Wenn K einer Beobachtung entspricht, hat sich H bewährt.

Allan Mustgrave hat kritisiert, dass Poppers Bild von der Bewährung von Hypothesen (in 3.2.) selbst auf einer "epistemischen Induktion" beruht:[9] Wenn eine Hypothese H1 bisher empirisch erfolgreicher war als eine konkurrierende Hypothese H2, dann ist die Annahme vernünftig, dass H1 auch in Zukunft erfolgreicher sein wird als H2. Dieses Prinzip der epistemischen Induktion ist unverzichtbar für empirische Wissenschaften im Allgemeinen und Poppers Methodologie im Speziellen. Denn würde man es nicht voraussetzen, wären alle unsere bisherigen Erfahrungen und Experimente irrelevant für unsere Zukunftsentscheidungen. Im Kern besagt es aber nichts anderes als das PUA!

Auch Popper muss also PUA voraussetzen und löst Induktionsproblem nicht.

Die induktiven Lösungsstrategien sind bestrebt, dass Induktionsproblem mit Hilfe der Induktion selbst zu lösen. Im Kern sehen diese immer so aus:

P1. In der Vergangenheit war die Zukunft so wie in der Vergangenheit.
K1. In der Zukunft wird die Zukunft so sein wie die Vergangenheit.

Diese Lösungsstrategie ist allerdings zirkulär. Denn einerseits will sie mit K1. Induktionsschlüsse und damit letztendlich auch PUA rechtfertigen. Andererseits ist der Schluss selbst nur gültig, wenn das PUA bereits vorausgesetzt wird:

P1. In der Vergangenheit war die Zukunft so wie in der Vergangenheit.
P2. Die Zukunft wird so sein wie die Vergangenheit.
K1. Ergo: In der Zukunft wird die Zukunft so sein wie die Vergangenheit.

Nun lehnen nicht alle erkenntnistheoretischen Positionen Zirkelschlüsse ab. Der Kohärentismus behauptet beispielsweise, dass zirkuläre Rechtfertigungen "regel-zirkulär" sein und dann einen epistemischen Wert haben können.[10][11]

Wesley C. Salmon hat diese Behauptung sehr überzeugend kritisiert: Er argumentiert, dass sich mit regelzirkulären Argumenten nicht nur die Reliabilität der Induktion, sondern auch die der "Anti-Induktion" begründen lässt:

Dabei besagt die Anti-Induktionsregel, dass ein Ereignis umso unwahrscheinlicher eintreten wird, je häufiger es bislang eingetreten ist und vice versa (PnUA). Das ist kontraintuitiv, aber nicht schlechter begründet als PUA![13]

Denn die Prämissen P1 und P1* werden durch dieselben Beobachtungen gestützt. Also kann man mit der regel-zirkulären Argumentation aufgrund derselben Datengrundlage zu widersprüchlichen Konklusionen kommen. Dies zeigt auf, dass es sich dabei um einen unzulässigen Argumentationstyp handeln muss. Damit sind aber auch die induktiven Lösungsstrategien zum Scheitern verurteilt.

Die abduktive Lösungsstrategie ist bestrebt, das Induktionsproblem mit Hilfe der Abduktion zu lösen. Im Kern basieren sie auf einem Schluss auf die beste Erklärung. Ein SBE schließt von Prämissen auf die beste Erklärung der Prämissen.

Wichtige Vertreter dieses Ansatzes sind Gilbert Harman[14], David Armstrong[15] und Peter Lipton[16]. Sie argumentieren, dass eine induktive Verallgemeinerung ein Spezialfall eines SBEs ist. Denn die beste Erklärung für "eine hohe Anzahl n aller bisher beobachteten Fs waren Gs" sei nun mal "Alle Fs sind Gs"![17]

Aber damit "Alle Fs sind Gs" die beste Erklärung sein kann, müssen wir das PUA wiederum voraussetzen. Wenn wir beispielsweise das PnUA voraussetzen, dann wäre "Alle übrigen Fs sind nicht Gs" die beste Erklärung für unsere Datenlage.

Die abduktiven Lösungsstrategien sind also genauso zirkulär wie die induktiven.

Hinzu kommen noch all die Probleme, die SBEs im Allgemeinen besitzen.

Die analytische Lösungsstrategie besagt, dass der Satz "der Induktionsschluss ist gerechtfertigt" analytisch und damit qua definitionem oder qua semantischer Konvention wahr ist. In Folge erweist sich das Induktions- als ein Scheinproblem.

Peter Strawson vergleicht induktive und deduktive Schlüsse. Er kommt zu dem Schluss, dass auch bei der Rechtfertigung der Deduktion Begründungszirkel unvermeidbar sind. Denn jede Art des logischen Schließens setzt bereits eine deduktive Logik voraus. Wenn wir logisches Denken und damit menschliches Denken also nicht ganz aufgeben wollen, müssen wir die Deduktion als rational definieren. Dann dürfen wir dasselbe aber auch mit der Induktion machen.

Aber diese Äquivalenz von Deduktion und Induktion ist irreleitend: Denn die Deduktion scheint in der Tat irgendwie a priori rational sein. Denn wir können uns schlichtweg keine Situation vorstellen, in der eine deduktive Schlussregel wie etwas der modus ponens nicht rational ist. Wir können uns aber sehr wohl welche vorstellen, in der verallgemeinernde Induktionsschluss nicht rational ist.

Es ist indes nicht nur vorstellbar, dass Induktionsschlüsse nicht rational sind, sie erweisen sich realiter vielfach als ungerechtfertigt! Etwa bei einem Glücksspieler, der die letzten acht Partien gewinnt und sich deswegen für unschlagbar hält. Induktionen sind also auch nicht analytisch oder apriori gerechtfertigt.

Nach diesen Ausführungen liegt die Vermutun nahe, dass induktive Schlüsse in der Tat nicht-demonstrativ bzw. nicht wahrheitsgarantierend sind.

Das heißt: Wenn die Prämissen eines induktiven Argumentes wahr sind, erzwingt dies nicht die Wahrheit seiner Konklusion. Aber vielleicht können induktive Schlüsse die Wahrheit ihrer Konklusionen begünstigen? Oder anders gefragt: Vielleicht sind induktive Schlüsse wahrheitsförderlich?

Die wahrscheinklichkeitstheoretische Lösungsstrategie ist bestrebt, das Induktionsproblem durch Rückgriff auf wahrscheinlichkeitshteoretische Konzepte abzuschwächen. Sie basieren im Detail meistens auf einem Bayesianismus.

Dabei sei die Stärke eines induktiven Argumentes p(K/D). Wobei "K" für die Konklusion und "D" für die zugrunde liegende Datengrundlage steht. Obwohl niemals gilt: p = 1, kann ein induktives Argument, je nach der Stärke seiner Datengrundlage D, die Wahrheit seiner Konklusion K mehr oder weniger wahrscheinlich machen. Fehlschlüsse können das hingegen nicht.

Aber nehmen wir einmal an, ein Würfel wird viele Male geworfen und bleibt in einem Sechstel aller Fälle mit zwei Augen nach oben liegen. Diese Beobachtung stellt nun unsere Datengrundlage D dar. Daraus basteln wir einen induktiven Schluss. Seine Konklusion K lautet offenbar, dass die Wahrscheinlichkeit für zwei Augen oben 1/6 beträgt. Zu K kann man durch verschiedene Regeln kommen:

a. a priori: A ist eines von sechs gleich-wahrscheinlichen Bs, also ist p(A) = 1/6.

b. induktiv: m/n aller beobachteten As waren Bs, also ist p(A) = m/n = 1/6.

Aufgrund einer anderen Schlussregel kommen wir aber zu einer ganz anderen Konklusion:

c. anti-induktiv: 1/6 aller As waren Bs, also ist p(A)=(n-m)/n = (6-1)/6 = 5/6.

Wir erinnern uns, dass die anti-induktive Schlussregel genauso gut begründet ist wie die induktive. Also kann der wahrscheinlichkeitstheoretische Ansatz wieder bei gleicher Datengrundlage D zu entgegengesetzten Resultaten führen: Bei b. ist D ein positiver, bei c. ein negativer Beleg für K und bei a. spielt D gar keine Rolle.

Der wahrscheinlichkeitstheoretische Ansatz muss also auch verworfen werden. Denn ein Ansatz, mit dem sich sowohl die positive Relevanz, die negative Relevanz als auch die Irrelevanz von D begründen lässt, kann nicht überzeugen.

Die in diesem Aufsatz untersuchten Lösungsstrategien konnten das Induktionsproblem allesamt nicht lösen.

Aber: Wir können aus dem Umstand, dass alle bisherigen Lösungsstrategien versagt haben, nicht schließen, dass auch die zukünftigen versagen werden. Das wäre ja selbst ein Induktionsschluss!

Die Diskussion um das Induktionsproblem ist also noch offen. Gehen wir aber für einen Moment davon aus, dass Hume Recht hätte. Was würde daraus folgen?

Dann wären Induktionsschlüsse nicht nur nicht-wahrheitsgarantierend bzw. nicht-demonstrativ, sondern nicht einmal wahrheitsförderlich! 

Das hieße: Dann machen die Prämissen eines induktiven Schlusses die Konklusion nicht nur mit p < 1, sondern sogar mit p = 0 wahrscheinlicher wahr.

Dann unterscheidet Induktionsschlüsse auch nichts mehr von Fehlschlüssen.

Folglich gibt es auch keinen rationalen Grund, S1 für plausibler zu halten als S2:

Das heißt aber auch: Wir können nicht nur keine gehaltserweiternde und demonstrative Schlüsse ziehen. Wir können auch prinzipiell und niemals gehaltserweiternde und auch nur plausible Schlussfolgerungen treffen!

Oder anders gesagt: Wenn Hume Recht hat, können wir durch logisches Nachdenken und Schließen niemals zu neuer Erkenntnis gelangen.

"Dann besteht zwischen geistiger Gesundheit und Geisteskrankheit kein Unterschied."
- Bertrand Russell: Philosophie des Abendlandes, S. 682.

Und selbst wenn man Humes Problem einmal beiseite lässt, steht die Induktion noch vor weiteren Problemen: Hempel-Paradoxon und Goodman-Paradoxon.

In der Wissenschaftsphilosophie stellte sich angesichts dieser massiven Probleme die drängende Frage, ob Wissenschaft im Rahmen eines sogenannten "Induktivismus" tatsächlich per Induktion charakterisiert werden kann und sollte.

Wissenschaft muss nämlich von Pseudowissenschaft differenziert werden können (Abgrenzungsproblem), was schwierig wird, wenn die ihr zugrundeliegenden Schlüsse nicht von Fehlschlüssen zu unterscheiden bzw. nicht plausibel sind.

Als direkte Antwort auf das Induktions- und das Abgrenzungsproblem charakterisierte der Wissenschaftsphilosoph Karl Popper Wissenschaft deduktiv:

àKritischer Empirismus

[1] David Hume: Eine Untersuchung über den menschlichen Verstand (1967), 80

[2] Der US-amerikanische Philosoph Charles Sanders Peirce war der erste, der Abduktion neben Induktion und Deduktion als eigenständigen Typus des Schließens diskutierte (The New Elements of Mathematics). Innerhalb der gegenwärtigen Diskussion ist auffällig, dass der Induktionsbegriff gelegentlich für jede Form nicht deduktiven Schließens verwendet wird und dementsprechend von enumerativen Induktionsschlüssen bis hin zu abduktiven Schlüssen alles umfasst, was nicht demonstrativ und gleichzeitig gehaltserweiternd ist. Ich werde mich dieser Terminologie jedoch nicht anschließen und immer, wenn abduktive Schlüsse gemeint sind, auch von abduktiven Schlüssen sprechen.

[3] Es muss nicht extra betont werden, dass dieses Ergebnis überaus kontraintuitiv erscheint. Führen wir uns die Gründe für diese Kontraintuitivität Schritt für Schritt vor Augen: Kaum jemand würde bestreiten, dass es inakzeptabel ist, von der Wahrheit des Hintersatzes eines Konditionals auf die Wahrheit des Vordersatzes zu schließen (Fehlschluss). Ein derartiger Schluss ist inakzeptabel, weil es offensichtlich ist, dass Flipper genauso gut ein Delfin (Meeressäuger) sein könnte. Außer Diskussion steht jedoch gleichzeitig, dass es nicht im selben Sinne irrational ist, auf der Basis der Beobachtung einer großen Menge von Hunden mit Lungen zu schließen, dass alle Hunde Lungen haben (enumerative Induktion). Natürlich wissen wir, dass auch Schlüsse dieser Art schiefgehen können. Aber im Gegensatz zum oben erwähnten Fehlschluss erscheint die Erwartung, dass sich in der Vergangenheit beobachtete Regelmäßigkeiten auch in Zukunft bewähren werden, angesichts unserer bisherigen Erfahrungen vollkommen rational zu sein. Wir schließen in genau dieser Weise, wenn wir wie selbstverständlich davon ausgehen, dass die Sonne, die bisher immer im Osten aufgegangen ist, auch morgen im Osten aufgehen wird. Und wir schließen in genau dieser Weiße, wenn wir unser Büro im sechsten Stock wie jeden Tag über das Treppenhaus und nicht durch das Fenster verlassen.

[4] Charlie D. Broad: Ethics and the History of Philosophy (1952), S. 143

[5] Vor den Hintergrund des Mach'schen Prinzips und den Problemen rund um dunkle Materie wird in der Tat eine variable Gravitationskonstante diskutiert.

[6] David Hume: Ein Traktat über die menschliche Natur I - III (1973), S. 46

[7] David Hume: Eine Untersuchung über den menschlichen Verstand (2007), S. 59

[8] Wesley C. Salmon: The Foundations of Scientific Inference (1967), S. 50.

[9] Allan Mustgrave: Karl Poppers Kritischer Rationalismus (2002), S. 25 - 42.

[10] David Papineau: Philosophical Naturalism (1993), Kap. 5.

[11] Stathis Psillos: Scientific Realism and the Aim of Science (1999), S. 82.

[12] Wesley C. Salmon: Should We Attempt to Justify Induction? (1957), S. 45 - 47.

[13] Denn der Induktivist könnte zwar entgegnen, dass sich das PnUA bisher nicht bewahrheitet und die Natur sich bislang äußerst gleichförmig verhalten hat.  Aber das bedeutet nicht, dass sich die Natur auch zukünftig gleichförmig verhalten wird. Dies würde das PUA voraussetzen. Und dieses kann vom Anti-Induktivisten mit demselben Recht abgelehnt werden wie PUA vom Induktivisten.

Die Entgegnung des Induktivisten für den Anti-Induktivisten fördert sogar noch dessen Induktionsskepsis. Denn wenn sich die Natur bislang gleichförmig verhalten hat, ist es laut PnUA umso wahrscheinlicher, dass sie es zukünftig nicht tun wird. Folglich sind das PUA und das PnUA gleich gut begründet!

[14] Gilbert Harman: The Inference to the best Explanation (1965), S. 88-95.

[15] David Malet Armstrong: What Is a Law of Nature (1983).

[16] Peter Lipton: Inference to the best Explanation (1991).

[17] Gemünzt auf unser Anfangsbeispiel bedeutet dies, dass die beste Erklärung für "alle 10 Millionen bisher beobachteten Schafe waren weiß" nun mal sein soll: "Überhaupt alle Schwäne sind weiß."

[18] Alfred J. Ayer: The Problem of Knowledge (1956), S. 74.

[19] Peter F. Strawson: Introduction to Logical Theory (1963), S. 249, 257.

Philpapers

Sanford Encyclopedia of Philosophy

David Humes über das Induktionsproblem

Goodmans-Paradoxon

Hempels-Paradoxon

Induktion

Induktivismus

Stand: 2019

Gliederung