Eine Reduktion ist eine Rückführung einer Entität A auf eine grundlegendere B.

Frage 1: Wie sind die Entitäten A und B ontologisch beschaffen?

a. Mikroreduktion: A ist ein Gesamtsystem und B seine Teile.

b. Theorienreduktion: A und B sind wissenschaftliche Theorien.

Frage 2: Was bedeutet es, dass A auf B reduziert wird?

a. ontologische Reduktion: A ist mit B identisch.

b. epistemische Reduktion: A ist durch B erklärbar.

c. semantische Reduktion: A und B sind gleichbedeutend.

Frage 3: Treten die Entitäten A und B gleichzeitig oder nacheinander auf?

a. synchrone Reduktion: A und B treten gleichzeitig auf.

b. diachrone Reduktion: A und B treten nacheinander auf.

Ein Reduktionismus behauptet entsprechend die Reduzierbarkeit von A auf B.

Eine Mikroreduktion liegt vor, gdw. die Eigenschaften eines Systems aus den Eigenschaften seiner Teile abgeleitet werden können. Das heißt aus:

a.    Den Eigenschaften der Teile in Isolation.

b.    Dem raumzeitlichen Arrangement der Teile.

c.    Den Wechselwirkungen zwischen den Teilen.

1. Beispiel Uhr: Eine Uhr besteht aus sichtbaren (Ziffernblatt, Zeiger, Knöpfe etc.) und unsichtbaren (Zahnräder, Schrauben, Feder etc.) Teilen. Das sichtbare Verhalten einer Uhr (Zeigerbewegung) kann mikroreduziert werden auf:

a.    die Eigenschaften der Bauteile Isolation (Form, Härte, etc.).

b.    Die raumzeitliche Anordnung der Bauteile (Aufbau der Uhr).

c.    Den Wechselwirkungen zwischen diesen Teilen (Mechanismus der Uhr).

2. Beispiel Temperatur: Die Temperatur eines Stoffes kann mikroreduziert  werden auf die mittlere kinetische Energie seiner Moleküle oder Atome. D.h. auf:

a.    Den Eigenschaften der Moleküle in Isolation.

b.    Dem raumzeitlichen Arrangement der Moleküle.

c.    Den Wechselwirkungen zwischen den Teilen.

Denn: Unser Temperaturbegriff erschöpft sich in einer kausalen Rolle. Und die mittlere Bewegungsenergie der Moleküle eines Stoffes spielt diese kausale Rolle. 

Frage: Sind alle materielle Entitäten auf ihre Teile mikroreduzierbar?

Das Putnam-Oppenheim-Schema bejaht diese Frage:

Es gibt aber insbesondere drei Phänomene, für die eine (ontologische oder epistemische) Nicht-Mikroreduzierbarkeit diskutiert wurde und wird:

1. Eigenschaften von lebendigen Systemen.

2. Eigenschaften von bewussten Systemen.

3. Eigenschaften von verschränkten Quantensystemen.

Eine klassische Theorienreduktion einer Theorie A auf eine Theorie B liegt nach Ernest Nagel vor, gdw. alle Gesetze der Theorie A logisch ableitbar sind aus:

a.    Den Gesetzen der Theorie A.

b.    Korrespondenzsätze für die Begriffe aus der Theorie B.

c.    Den Systemspezifikationen bzw. Umständen.

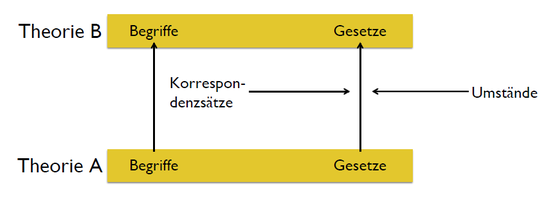
BSP: Die anorganische Chemie ist theorienreduzierbar auf die Quantenmechanik.

Denn nehmen wir z.B. dieses Gesetz G aus der anorchanischen Chemie:

G. Elemente der 1. Hauptgruppe reagieren stark mit Elementen aus der 7. Hauptgruppe (z.B. Natrium und Chlor zu NaCl). Dann ist G logisch ableitbar aus:

a.    Den Gesetzen der Quantenmechanik.

b.    Korrespondenzsätze, die chemischen Begriffen wie "Elemente aus der 1. Hauptgruppe" oder "stark reagieren" quantenmechanische Begriffe wie "Stoff mit der Mikrostruktur M" oder "viel Energie freisetzen" zuweisen.

c.     Systemspezifikationen (Druck, Temperatur, etc.).

Weitere Beispiele:

1.    Die Strahlenoptik kann theorienreduziert werden auf die Wellenoptik und diese kann theorienreduziert werden auf Quantenoptik.

2.    Die Thermodynamik kann theorienreduziert werden auf die statistische Mechanik.

3.    Das Galileische Fallgesetz kann theorienreduziert werden auf die Newton’sche Mechanik und diese kann theorienreduziert werden auf die Relativitätstheorie.

Aber: Bereits bei den Beispielen 1. bis 3. ist keine strikte logische Ableitbarkeit gegeben. Die Relativitätstheorie bspw. liefert nur näherungsweise gleiche Vorhersagen für Geschwindigkeiten gegen Null wie die Newtonsche Mechanik.

Und: Die Beispiele 1. bis 3. sind alle aus der Physik. Andere Disziplinen, in denen die mathematische Exaktheit fehlt, wie etwa die Biologie oder gar die Soziologie haben noch größere Schwierigkeiten mit einer nagelschen Theorienreduktion.

Wegen all dieser Probleme wird Nagels "klassisches" Modell nicht mehr vertreten.

Ein neueres und besseres Modell findet sich bei Cliff A. Hooker.

Für Kritik an Type-Theorienreduktionen siehe: Multirealisierbarkeitsargument

Eine ontologische Reduktion von A auf B liegt vor, gdw. A und B identisch sind.

Frage: Was soll das bedeuten?

i. Konsulidierung: Entität A ist eigentlich Entität B.

ii. Elimination: Entität A gibt es gar nicht.

These 1: Eine Uhr A kann ontologisch-mikroreduziert werden auf seine Teile B.

i. Konsulidierung: Die Uhr ist nicht mehr als die Summe ihrer Teile.

ii. Elimination: Die Uhr gibt es gar nicht, es gibt nur die Teile.

These 2: Das Universum kann ontologisch-mikroreduziert werden auf die in ihm befindlichen Elementarteilchen.

i. Konsulidierung: Das Universum ist nicht mehr als die Summe der in ihm befindlichen Elementarteilchen. Siehe auch: Monismus.

ii. Elimination: Den Kosmos gibt es gar nicht, es gibt nur kleinste Teilchen. Siehe auch: Mereologischer Nihilismus.

These 3: Mentale Eigenschaften sind identisch mit physischen Eigenschaften.

i. Identitätstheorien: Mentale Eigenschaften sind physische Eigenschaften.

ii. Eliminationstheorien: Es gibt nur physische Eigenschaften.

Für Kritik an These 3i. siehe: Saul Kripke über die Identitätstheorie.

Für Kritik an These 3ii. siehe: Kritik am Eliminativen Physikalismus.

Eine epistemische Reduktion von A auf B liegt vor, gdw A durch B erklärbar ist.

Man spricht daher häufig auch von einer explanatorischen Reduktion.

Und: A ist durch B erklärbar, gdw. Wissen über A mit Wissen über B identisch ist.

These 1: Eine Uhr A kann epistemologisch-mikroreduziert werden auf die Teile B.

Das würde bedeuten: Wenn ich alles über die Eigenschaften der Teile B, ihrem Arrangement und ihren Wechselwirkungen weiß, weiß ich auch alles über die Uhr.

These 2: Das Universum kann epistemisch-mikroreduziert werden auf die in ihm befindlichen Elementarteilchen.

Das würde bedeuten: Die Elementarteilchenphysik kann alle kosmischen Eigenschaften erklären und damit als universelle Einheitswissenschaft fungieren.

These 3: Mentale Eigenschaften können epistemisch-reduziert werden auf physische Eigenschaften.

Das würde bedeuten: Eine physische Eigenschaft wie "Peter hat feuernde C-Fasern" erklärt vollumfänglich eine mentale Eigenschaft wie "Peter sieht Gelb."

Für Kritik an These 3 siehe: Joseph Levines Argument der Erklärungslücke.

Eine diachrone Reduktion von A auf B liegt vor, gdw. A und B nacheinander auftreten. Häufigere (aber uneingängigere) Bezeichnung: sukzessive Reduktion.

Beispiel 1: Die Spezielle Relativitätstheorie ist diachron-theorienreduzierbar auf die historisch vorangegegangene klassische Mechanik im Limes V à 0.

Beispiel 2: Die Quantenmechanik ist evtl. diachron-theorienreduzierbar auf die historisch vorangegangene klassische Mechanik im Limes hoher Quantenzahlen.

Der diachrone Reduktionsbegriff enthält also zwei Bedeutungskomponenten: den des Zurückführens und den des Verringerns (i.S.v: Verkleinern, Vereinfachen).

Beispiel 1 & 2: Die Spezielle Relativitätstheorie und die Quantenmechanik werden bei ihrer diachronen Reduktion auf die klassische Mechanik nicht nur auf diese zurückgeführt, sondern ihr Geltungsbereich auch massiv verkleinert.

Die neuartigen Gesetze der SRT und der QM bei hohen Geschwindigkeiten oder niedrigen Quantenzahlen gehen dabei also komplett verloren. Das ist aber intendiert, da es ja um die Frage geht, ob sich die mathematischen Vorhersagen der SRT und QM im Geltungsbereich der klassischen Mechanik dieser annähern.

Merke: Wenn A auf B diachron-theorienreduziert wird, dann ist der Gegenstands-bereich von A in der Regel eine Teilmenge des Gegenstandsbereiches von B.

Eine synchrone Reduktion von A auf B liegt vor, gdw. A und B gleichzeitig auftreten. Häufigere (aber uneingängigere) Bezeichnung: interlevel Reduktion.

Wenn A synchron-ontologisch reduzierbar ist auf B, dann supervenieren die B-Eigenschaften über (das heißt: werden bestimmt durch) die A-Eigenschaften.

Merke: Supervenienz ist nur notwendig, nicht hinreichend für Reduzierbarkeit.

Also: Ein Antireduktionismus kann:

entweder bestreiten, dass B über A superveniert, denn das wäre notwendig dafür, dass A auf B reduzierbar ist.

oder akzeptieren, dass B über A superveniert, aber behaupten, dass A weiterhin über B emergiert oder substantiell verschieden gegenüber B ist.

Internet Encyclopedia of Philosophy
Philpapers

Stanford Encyclopedia of Philosophy

Emergenz

Holismus

Pro- und Contra

Substanzdualismus

Stand: 2019

Gliederung