Eine wissenschaftliche Vorhersage ist ein aus einer wissenschaftlichen Theorie T abgeleiteter Beobachtungssatz S(p) über ein Phänomen p des Typs P.

Dabei ist eine Vorhersage erfolgreich, genau dann wenn S(p) wahr ist.

Formale Explikation:

T prognostiziert erfolgreich ein Phänomen p des Typs P, gdw. gilt:
a. Prognosebedingung: T ⊢ S (p) (sprich: T ableitbar Satz über p).
b. Erfolgsbedingung: S (p) ist wahr, d.h. es ist der Fall, dass p.

Sehen wir uns ein paar Beispiele an:

Die Allgemeine Relativitätstheorie postuliert eine nicht-direkt beobachtbare Krümmung der Raumzeit durch massebehaftete Körper. Dadurch konnte sie erstens erfolgreich die bereits bekannte Ablenkung des Merkurperihels vorhersagen. Zweitens den bis dahin völlig unbekannten Lichtablenkungseffekt.

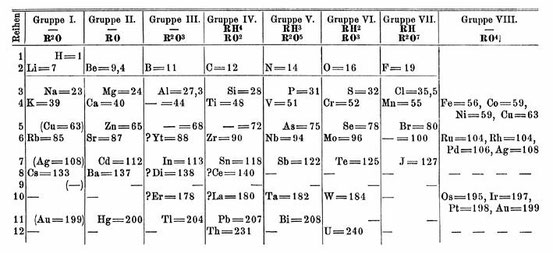
Das erste Periodensystem von Dmitri Iwanowitsch Mendelejew enthielt bereits 66 Elemente. Mit diesem konnte Mendelejew erstens die Atommassen der damals bekannten 63 Elemente vorhersagen. Und er konnte auch die Atommasse der bis dahin unbekannten Elemente Gallium, Scandium und Germanium vorhersagen.

Die Astronomen im altertümlichen Babylon konnten bestimmte Periodizitäten in astronomischen Phänomenen beobachten. Anschließend entwickelten sie algebraische Regeln, um diesen Phänomentyp zu beschreiben. Aufgrund dieser Regeln konnten sie dann wahre Sätze über Phänomene desselben Typs ableiten.

Nun können wir zwei Arten von Prognoseerfolgen unterscheiden: 

Eine Akkomodation liegt vor, gdw. P nicht unabhängig gegenüber T ist.

Eine Prädikation liegt vor, gdw. P unabhängig gegenüber T ist.

Der Prognoseerfolg der babylonischen Astronomen war eine Akkomodation. Die erfolgreiche Prognose des Lichtablenkungseffekts klar eine Prädiktion. Intuitiv  bestätigen Prädiktionen Theorien stärker als Akkomodationen. Aber stimmt das?

Hier können drei Ansichten unterschieden werden:

starker Prädiktivismus: Ein Prädiktionserfolg bestätigt eine Theorie, ein Akkomodationserfolg hingegen nicht.

Prädiktivismus: Ein Prädikaitonserfolg bestätigt eine Theorie stärker als ein Akkomodationserfolg.

Akkomodationismus: Eine Prädiktionserfolg bestätigt eine Theorie nicht stärker als eine Akkomodationserfolg.

Es können die folgenden Erklärungsansätze unterschieden werden:

Zufall: Die Vorhersage von p war zufällig erfolgreich.

Wahrheit: Die Vorhersage von p war erfolgreich, weil T wahr ist.

Design: Die Vorhersage von p war erfolgreich, weil T designed wurde, um Phänomene des Typs P vorherzusagen.

Das ´no-coincidence argument´ geht nun so:

Ein Prädiktionserfolg kann entweder durch den Zufallsansatz oder durch den Wahrheitsansatz erklärt werden. Der Wahrheitsansatz ist zweifellos der bessere Erklärungsansatz. Also sollten wir Prädiktionserfolge von Theorien durch ihre Wahrheit erklären, demzufolge sind Prädiktionserfolge bestätigend.

Ein Akkomodationserfolg kann durch die Designansatz oder durch den Wahrheitsansatz erklärt werden. Der Designansatz wird allgemein als explanatorisch ausreichend akzeptiert. Den Wahrheitsansatz zusätzlich zu bemühen, wäre redundant und wir wollen Redundanz vermeiden. Also sollten wir Akkomodationserfolge von Theorien ausschließlich durch den Designansatz erklären, demzufolge sind Akkomodationserfolge nicht bestätigend.

Nach diesem Argument sind Prädiktionserfolge also bestätigend und Akkomodationserfolge nicht. Insofern ist es ein Argument für den Prädiktivismus.

Kritik: Eric Barnes den Einwand angebracht, dass die Wahrheit einer Theorie und die Absichten eines Theoretikers verschiedene Dinge erklären:[1] Die Wahrheit einer Theorie erklärt, warum ihre Vorhersagen wahr sind, während die Absichten eines Theoretikers erklären, warum die Theorie ausgewählt wurde.

Wir können uns hier zwei Szenarien vorstellen:

Fall a. T prädiktiert p erfolgreich, gdw.:
(1) T ⊢ S (p);
(2a) T wurde nicht designed, um S(p) vorzusagen;

(3) S(p) ist wahr.

Fall b. T akkomodiert E, gdw.:
(1) T ⊢ S (p);
(2b) T wurde designed, um S(p) vorherzusagen;
(3) S(p) ist wahr.

Der Wahrheitsansatz kann (3) in beiden Fällen und zwar gleich gut, aber nicht (1) und nicht (2) erklären. Angenommen also eine Theorie T ist wahr. Dann ist das ein guter Ansatz um zu erklären, warum ein daraus abgeleiteter Beobachtungssatz S(p) ebenfalls wahr ist. Es erklärt aber nicht die logische Relation T ⊣ S (p). Und es erklärt auch nicht, dass T designed wurde oder nicht.

Der Designansatz kann in beiden Fällen (1) und (3) nicht erklären. Da (1) eine logische Relation zwischen T und P ausdrückt, das heißt T ⊣ S (p), egal ob T designed wurde oder nicht. Und (3) drückt eine Korrespondenzrelation zwischen dem Gehalt von S(p) und p aus, das heißt S(p) ist wahr, egal ob T designed wurde oder nicht. Der Designansatz kann auch nicht (2a) erklären, da beide im Widerspruch stehen. Er kann auch nicht (2b) erklären, da er (2b) nur wiederholt.

Also: Der Wahrheitsansatz erklärt (3) in beiden Fällen gleich gut. Der  Design-ansatz erklärt hingegen gar nichts. Er kann den Wahrheitsansatz im Fall b also auch nicht überflüssig machen. Nach Barnes schlägt dieses Argument also fehl.

David Harker hat ein "Epistemische Werte Argument" hervorgebracht.[] Nach Harker bestätigen Prädiktionserfolge eine Theorie tatsächlich häufig stärker als Akkomodationserfolg. Das liegt aber an bestimmten epistemischen Werten, nicht weil Prädiktionserfolge selbst eine stärkere Bestätigungskraft besäßen.

Nach Harker wollen wir Theorien, die mehr erklären und weniger voraussetzen. Die babylonischen Astronomen mussten einige ad-hoc Hypothesen einführen, um ein zukünftiges Phänomen akkomodieren zu können. Die Allgemeine Relativitätshteorie hingegen gilt als gut bestätigt, weil sie aufgrund weniger Annahmen viele Phänomene erklären konnte. Der Prädiktionserfolg der ART schneidet in Sachen Erklärungsstärke- und einfachheit also besser ab als der Akkomodationserfolg der Babyloner. Deshalb war erster stärker bestätigend.

Kritik: Einfachheit ist kein epistemischer sondern ein pragmatischer Wert. Warum sollten wir einfache Theorien epistemisch bevorzugen? Dafür müssten wir a prior wissen, dass die unerforschte Welt einfach beschaffen ist, was wir nicht tun. Also werden einfache Theorien durch Prognoseerfolge nicht stärker bestätigt.

Der Prädiktivist muss eine Explikation von "unabhängige Prognoseerfolge" anbieten. Diese enthält in der Regel eine zweistellige Relation zwischen T und P.

a. Die erfolgreiche Prognose des Phänomens p des Typs P aus der Theorie T ist historisch-unabhängig, gdw. P unbekannt war, als T konstruiert wurde.

b. Die erfolgreiche Prognose des Phänomens p des Typs P aus der Theorie T ist epistemisch-unabhängig, gdw. P unter den Wissenschaftlern unbekannt war, als diese T konstruiert haben.

Kritik: Diese beiden Definitionen sind wohl zu restriktiv. Denn die erfolgreiche Vorhersage des Merkurperihels durch die ART war bspw. keine historisch oder epistemisch neurartige Vorhersage. Dennoch gilt sie als eine starke Bestätigung der ART. Denn, so könnte man argumentieren, Einstein war das Phänomen zwar bekannt, aber er hat dieses Wissen bei der Konstruktion der ART nicht gebraucht.

c. Die erfolgreiche Prognose des Phänomens p des Typs P aus der Theorie T ist gebrauchsunabhängig, gdw. die Wissenschaftler kein Wissen um P gebraucht haben, um T zu konstruieren. (Vertreter: John Worrall[4])

Kritik: Diese Definition ist auch zu restriktiv. Denn angenommen die Zwillings-

wissenschaftler Tim und Tom konstruieren unabhängig voneinander dieselbe Theorie T zum Zeitpunkt t1. Sie arbeiten unter den gleichen epistemischen Bedingungen, mit dem einzigen Unterschied, dass Tom sein Kenntnis über P gebraucht hat um T zu konstruieren und Tim nicht. Durch T lässt sich erfolgreich das Phänomen p des Typs P zum Zeitpunkt t2 prognostizieren. Der Prognoseerfolg von Tims Theorie scheint gebrauchsneuartig und der von Toms Theorie scheint es nicht – das ist aber unmöglich, da es sich um dieselbe Theorie T handelt![L]

Replik: Tom hat seine Kenntnis über P bei der Konstruktion von T offensichtlich in einer nicht-wesentlichen Weise gebraucht. Denn Tim hat auch ohne den Gebrauch von P dieselbe Theorie T konstruieren können. Daraus folgt, dass Tom T prinzipiell auch dann hätte konstruieren und p mit T vorhersagen können (genauso wie Tim es tat), wenn er seine Kenntnis über P nicht bei der Konstruktion von T verwendet hätte. Dabei scheint nicht nur Tims tatsächlicher Prognoseerfolg, sondern auch dieser kontrafaktische Umstanfd dafür zu sorgen, dass die erfolgreiche Prognose von p aus T diese Theorie bestätigt.

d. Die erfolgreiche Prognose des Phänomens p des Typs P aus der Theorie T1 ist essentiell-gebrauchsneuartig, wenn gilt:

- Unabhängigkeit: Es gibt eine minimale adäquate Rekonstruktion des rationalen Prozesses, der zu T1 führt und ohne Kenntnis von P auskommt,

- Einzigartigkeit: Es gab zum Zeitpunkt der erfolgreichen Vorhersage von p durch T1 keine mit T1 inkompatible Theorie T2, die in der Lage war p zu prognostizieren oder Gründe für die Erwartbarkeit von p zu geben.[123]

(Vertreter: Jarrett Leplin)

Kritik: Diese Definition ist immer noch zu restriktiv. Angenommen Lia hat die Theorie T1 zu t1 entworfen und ihre Lea hat zum späteren Zeitpunkt t2, aber völlig unabhängig von Lia, eine mit T1 inkompatible Theorie T2 konstruiert. Die Theorien T1 und T2 prognostizieren ebenfalls unabhängig voneinander erfolgreich das Phänomen p des Typs P. Dann ist der Prognoseerfolg von Lia essentiell neuartig und der von Lea ist es nicht. Dass liegt aber einzig und allein daran, dass Lia ihre Theorie vor Lea konstruiert hat. Dieser historisch kontingente Umstand darf aber keinen Einfluss darauf haben, dass T1 besser bestätigt ist als T2. Denn dies würde den Entstehungs- und Rechtfertigungszusammenhang von wisseenschaftlichen Theorien vermischen. Es droht ein genetischer Fehlschluss.

e. Die erfolgreiche Prognose des Phänomens p des Typs P1 durch die Theorie T_i  und die Zusatzannahmen {…Ai…} ist funktional- neuartig, gdw.
ein Datensatz ODi  existiert, der nur direkte Beschreibungen oder induktive Verallgemeinerungen von empirischen Phänomentypen P2, … Pn beinhaltet, wobei eine Beschreibung von P1 nicht in ODi  enthalten ist. Es ist möglich durch induktive (abduktive) Schlüsse von OD i zu T und {…Ai…} zu gelangen. In diesem Sinne sind T und {…Ai…} funktional unabhängig von P.
(Vertreter: Mario Alai)

Das ist meiner Ansicht nach der bisher beste Explikationsversuch.

Stand: 2019

Aufsätze