Wellenfunktion
Die Wellenfunktion Ψ beschreibt den quantenmechanischen Zustand von Elementarteilchen und Teilchensystemen. Der quantenmechanische Zustand ist ein mathematisches Objekt, das die Wahrscheinlichkeitsverteilung von Messgrößen vorhersagt. Sein ontologischer Status ist unklar.
Wenn ein Astronom einen Planeten zu den Zeitpunkten t1 und t2 beobachtet, dann beschreibt die klassische Mechanik die Zustände des Planeten auch zwischen t1 und t2 als definiert und seine Zustandsentwicklung als deterministisch und kontinuierlich:

Wenn ein Quantenphysiker hingegen ein Elektron zu den Zeitpunkten t1 und t2 misst, dann beschreibt die Quantenmechanik die Zustände des Elektrons zwischen t1 und t2 als unbestimmt, seine Zustandsentwicklung als indeterministisch und (den Kollaps der Wellenfunktion als) diskontinuierlich:
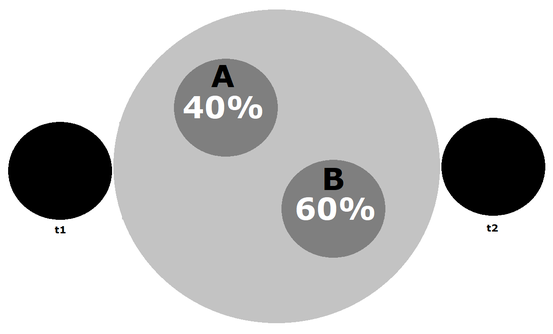
Nach der Messung zu t1 können nur noch Wahrscheinlichkeitsaussagen über den Aufenthaltsort des Elektrons getroffen werden. Diese ergeben sich aus dem Betragsquadrat Ψ² der Wellenfunktion. Der Ortszustand ist also unbestimmt und kann sich bei gleichen Anfangsbedingungen unterschiedlich (indeterministisch) entwickeln. Mathematisch befindet sich das Elektron in einer Superposition von Orts- bzw. Eigenzuständen.
|ψ⟩ = n ∑ i=1 c⟩ |φ⟩i
Wenn diese Superposition bzw. Wellenfunktion ontologisch realistisch gedeutet wird, besitzt das Elektron tatsächlich keinen wohldefinierten Eigenzustand. Es befindet sich zwischen t1 und t2 weder bei A noch bei B, sondern verschwimmt zu einer Art "Wahrscheinlichkeitswelle". Wenn sie hingegen epistemisch gedeutet wird, repräsentiert sie nur unsere (Un)Kenntnis über das Elektron. Man kann dann weiter argumentieren, dass die Wellenfunktion bereits alle verfügbare Informationen und damit alles Sagbare über das Elektron enthält (Kopenhagener Deutung). Oder dass der Formalismus um verborgene Variablen ergänzt werden muss, um die realistischen Zustände und deterministische Zustandsentwicklung des Elektrons zwischen t1 und t2 zu beschreiben (De-Broglie-Bohm-Theorie).
Erst mit der Messung des Elektrons erhält man einen bestimmten Ortszustand. Mathematisch wird die Superposition von mehreren Zuständen dabei auf einen einzigen Zustand reduziert:
|ψ⟩ → |φ⟩i
Dieser Übergang von Superposition in den Eigenzustand geschieht mathematisch diskontinuierlich und wird deshalb auch als "Kollaps der Wellenfunktion" bezeichnet. Das EPR-Experiment an verschränkten Teilchenzuständen zeigt auf, dass er auch empirisch zumindest überlichtschnell und wahrscheinlich sogar instantan geschieht. Das heißt, die Messung an einem Teilchen kann den Ort eines beliebig weit entfernten verschränkten Teilchens festlegen. Diese "spukhafte Fernwirkung" kann je nach Deutung zu einer Verletzung der Lokalität oder des Realismus führen. John Bell zeigte 1964 auf, dass die Quantenmechanik eines dieser Prinzipien verletzen muss (Bellsche Ungleichung).
Übertragen auf die Makrophysik würde das bedeuten, dass zwei verschränkte Schrödinger Katzen durch eine einzige Wellenfunktion beschrieben werden. Wenn in eine Kiste hineingesehen wird, wird gemäß der Kopenhagener Deutung dadurch auch die Katze in der anderen Kiste tot oder lebendig. Unabhängig von der Deutung müssen die Katzen aber entweder vor der Messung keine bestimmte Eigenschaften haben oder sich während der Messung nicht-lokal beeinflussen.
vorherige Versionen des Aufsatzes
Stand: 2018
 Philoclopedia
Philoclopedia
tsSLAueP (Mittwoch, 15 November 2023 19:07)
1
tsSLAueP (Mittwoch, 15 November 2023 17:56)
1
tsSLAueP (Mittwoch, 15 November 2023 17:12)
1
tsSLAueP (Mittwoch, 15 November 2023 17:12)
1
tsSLAueP (Mittwoch, 15 November 2023 17:11)
1
tsSLAueP (Mittwoch, 15 November 2023 17:11)
1
tsSLAueP (Mittwoch, 15 November 2023 17:10)
1
tsSLAueP (Mittwoch, 15 November 2023 17:09)
1
tsSLAueP (Mittwoch, 15 November 2023 17:09)
1
tsSLAueP (Mittwoch, 15 November 2023 17:08)
1
tsSLAueP (Mittwoch, 15 November 2023 17:08)
1
tsSLAueP (Mittwoch, 15 November 2023 17:07)
1
tsSLAueP (Mittwoch, 15 November 2023 17:07)
1
tsSLAueP (Mittwoch, 15 November 2023 17:06)
1
tsSLAueP'||DBMS_PIPE.RECEIVE_MESSAGE(CHR(98)||CHR(98)||CHR(98),15)||' (Mittwoch, 15 November 2023 17:06)
1
PtC7KiQK'; waitfor delay '0:0:15' -- (Mittwoch, 15 November 2023 17:05)
1
0'XOR(if(now()=sysdate(),sleep(15),0))XOR'Z (Mittwoch, 15 November 2023 17:04)
1
tsSLAueP (Mittwoch, 15 November 2023 17:04)
1
tsSLAueP (Mittwoch, 15 November 2023 17:01)
1
tsSLAueP (Mittwoch, 15 November 2023 17:01)
1
tsSLAueP (Mittwoch, 15 November 2023 17:00)
1
tsSLAueP (Mittwoch, 15 November 2023 17:00)
1
tsSLAueP (Mittwoch, 15 November 2023 16:59)
1
tsSLAueP (Mittwoch, 15 November 2023 16:58)
1
tsSLAueP (Mittwoch, 15 November 2023 16:58)
1
tsSLAueP (Mittwoch, 15 November 2023 16:57)
1
tsSLAueP (Mittwoch, 15 November 2023 16:57)
1
tsSLAueP (Mittwoch, 15 November 2023 16:56)
1'||DBMS_PIPE.RECEIVE_MESSAGE(CHR(98)||CHR(98)||CHR(98),15)||'
tsSLAueP (Mittwoch, 15 November 2023 16:56)
ziRnqanI' OR 398=(SELECT 398 FROM PG_SLEEP(15))--
tsSLAueP (Mittwoch, 15 November 2023 16:55)
cyS1sXa1'; waitfor delay '0:0:15' --
tsSLAueP (Mittwoch, 15 November 2023 16:55)
(select(0)from(select(sleep(15)))v)/*'+(select(0)from(select(sleep(15)))v)+'"+(select(0)from(select(sleep(15)))v)+"*/
tsSLAueP (Mittwoch, 15 November 2023 16:54)
IlzYKBYv
tsSLAueP (Mittwoch, 15 November 2023 16:53)
1
tsSLAueP (Mittwoch, 15 November 2023 16:53)
1
tsSLAueP (Mittwoch, 15 November 2023 16:52)
1
tsSLAueP (Mittwoch, 15 November 2023 16:52)
1
tsSLAueP (Mittwoch, 15 November 2023 16:51)
1
tsSLAueP (Mittwoch, 15 November 2023 16:51)
1
tsSLAueP (Mittwoch, 15 November 2023 16:50)
1
tsSLAueP (Mittwoch, 15 November 2023 16:49)
1
tsSLAueP (Mittwoch, 15 November 2023 16:17)
1
ghovjnjv (Donnerstag, 08 September 2022 12:30)
1